�ڶ�ʮһ��21.1һԪ���η��̵�һ���
�٢�
�ڶ�ʮһ��21.1һԪ���η��̵ڶ����
2x2-6x-1=0��2��-6
�ڶ�ʮһ��21.1һԪ���η��̵������
k��-4
�ڶ�ʮһ��21.1һԪ���η��̵������
2��-2
�ڶ�ʮһ��21.1һԪ���η��̵������
1
�ڶ�ʮһ��21.1һԪ���η��̵������
-3
�ڶ�ʮһ��21.1һԪ���η��̵������
-3
�ڶ�ʮһ��21.1һԪ���η��̵������
�⣺ÿ֧��Ӷ���Ҫ�������������x-1������
������֮��ֻ��1�����������Կ��з���Ϊ��
1/2x��x-1��=4��7
����һԪ���η��̵�һ����ʽ��x2-x-56=0
�ڶ�ʮһ��21.1һԪ���η��̵ڰ����
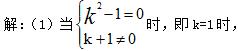
���̣�k2-1��x2-��k+1��x+k=0��һԪһ�η���-2x+1=0
��2������k2-1����0ʱ����k�١�1ʱ�����̣�k2-1��x2-��k+1��=0
��һԪ���η��̷��̵Ķ�����ϵ����k2-1��һ����ϵ����-��k+1������������k

 ��ʦ�����꼶�ϲ���ѧ��ҵ���𰸽���ʡ
��ʦ�����꼶�ϲ���ѧ��ҵ���𰸽���ʡ �˽̰���꼶�ϲ�Ӣ����ҵ���𰸽���ʡ
�˽̰���꼶�ϲ�Ӣ����ҵ���𰸽���ʡ �˽̰���꼶�ϲ���ѧ��ҵ���𰸽���ʡ
�˽̰���꼶�ϲ���ѧ��ҵ���𰸽���ʡ �̿ư���꼶�ϲ�������ҵ���𰸽���ʡ
�̿ư���꼶�ϲ�������ҵ���𰸽���ʡ �˽̰���꼶�ϲ�������ҵ���𰸽���ʡ
�˽̰���꼶�ϲ�������ҵ���𰸽���ʡ ���꼶�ϲữѧ�α��𰸻��̰�
���꼶�ϲữѧ�α��𰸻��̰� ����ʦ�����꼶�ϲ���ѧ���
����ʦ�����꼶�ϲ���ѧ��� �˽̰���꼶�ϲữѧ���
�˽̰���꼶�ϲữѧ��� �˽̰���꼶�ϲ��������
�˽̰���꼶�ϲ�������� �˽̰���꼶�ϲ�Ӣ�����
�˽̰���꼶�ϲ�Ӣ����� ��̰���꼶�ϲ��ѧ���
��̰���꼶�ϲ��ѧ��� ���ư���꼶�ϲ���ѧ���
���ư���꼶�ϲ���ѧ��� ��̰���꼶�ϲ���ѧ���
��̰���꼶�ϲ���ѧ��� �˽̰���꼶�ϲ��������
�˽̰���꼶�ϲ�������� ��ʦ�����꼶�ϲ���ѧ���
��ʦ�����꼶�ϲ���ѧ��� �˽̰���꼶�ϲ���ʷ֪ʶ������ѵ����
�˽̰���꼶�ϲ���ʷ֪ʶ������ѵ���� ���꼶�ϲ����Ŀο������ս̰�
���꼶�ϲ����Ŀο������ս̰� �տư���꼶�ϲ���������ϰ���
�տư���꼶�ϲ���������ϰ��� ���꼶�ϲ�����ѧ������Ұ���˽̰�
���꼶�ϲ�����ѧ������Ұ���˽̰� ��̰���꼶�²���ѧ�α���
��̰���꼶�²���ѧ�α��� ���꼶�²ữѧ�±����ѵ�����˽̰�
���꼶�²ữѧ�±����ѵ�����˽̰� ���꼶�²ữѧ���³�̰�
���꼶�²ữѧ���³�̰� ���꼶�ϲ���ʷͬ��������������˽̰�
���꼶�ϲ���ʷͬ��������������˽̰� ���꼶�ϲ�����ͬ����ϰ���ս̰�
���꼶�ϲ�����ͬ����ϰ���ս̰� ���꼶�²�����ͬ����ϰ���տư�
���꼶�²�����ͬ����ϰ���տư�