八年级下册数学同步解析与测评18.2特殊的平行四边形答案人教版

18.2特殊的平行四边形同步学习（一）第一题答案

D

18.2特殊的平行四边形同步学习（一）第二题答案

C

18.2特殊的平行四边形同步学习（一）第三题答案

10

18.2特殊的平行四边形同步学习（一）第四题答案

5

18.2特殊的平行四边形同步学习（一）第五题答案

设AB = x，则BD = 4 + x，由勾股定理，

得x²+ 8²= （x + 4)²，解得x = 6，即AB的长度为6 cm.

由S△ABD = AB·AD = AE·BD，可得AE = 4.8，即点A到BD的距离为4.8 cm.

18.2特殊的平行四边形同步学习（二）第一题答案

C

18.2特殊的平行四边形同步学习（二）第二题答案

C

18.2特殊的平行四边形同步学习（二）第三题答案

∠A = 90°或者AC = BD

18.2特殊的平行四边形同步学习（二）第四题答案

BC = 2AB

18.2特殊的平行四边形同步学习（二）第五题答案

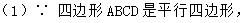
18.2特殊的平行四边形同步学习（三）第一题答案

A

18.2特殊的平行四边形同步学习（三）第二题答案

C

18.2特殊的平行四边形同步学习（三）第三题答案

96 cm²；4OCm

18.2特殊的平行四边形同步学习（三）第四题答案

2.4 cm

18.2特殊的平行四边形同步学习（三）第五题答案

提示：先证△CBE ≌ △CDE，

∴ ∠CBE = ∠CDE，再由AB∥CD，

∴ ∠AFD = ∠CDE，

∴ ∠AFD = ∠CBE

18.2特殊的平行四边形同步学习（四）第一题答案

D

18.2特殊的平行四边形同步学习（四）第二题答案

B

18.2特殊的平行四边形同步学习（四）第三题答案

连接AC，BD

∵ E，F，G，H分别是AD，AB，BC，CD的中点，

∴ EF ∥= ½BD，GH ∥= ½BD，EH ∥= ½AC，FG ∥= ½AC.

由矩形ABCD，可得AC = BD，

∴ EF = FC = GH = EH，

∴ 四边形EFGH是菱形.

18.2特殊的平行四边形同步学习（四）第四题答案

提示：由四边形ABCD是平行四边形，且EF垂直平分AC，可证△AOE ≌ △COF，

∴ EO = FO.又AO = CO，

∴ 四边形AFCE是平行四边形.再由AC ⊥ EF，可得□AFCE是菱形.

18.2特殊的平行四边形同步学习（五）第一题答案

B

18.2特殊的平行四边形同步学习（五）第二题答案

C

18.2特殊的平行四边形同步学习（五）第三题答案

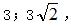
18.2特殊的平行四边形同步学习（五）第四题答案

75°

18.2特殊的平行四边形同步学习（五）第五题答案

（1）提示：由四边形ABCD是正方形，且DE = BF，可证△ADE ≌ △ABF，

∴ ∠EAD = ∠FAB 

∵ ∠EAD + ∠EAB = 90°，

∴ ∠FAB + ∠EAB = 90°，

∴ AE ⊥ AF

（2）提示：由（1）可得AE ⊥ AF，且AE = AF.由勾股定理，

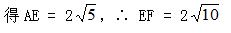
18.2特殊的平行四边形同步学习（六）第一题答案

D

18.2特殊的平行四边形同步学习（六）第二题答案

一个角是直角且一组邻边相等，或者对角线垂直且相等.

18.2特殊的平行四边形同步学习（六）第三题答案

提示：由四边形ABCD是正方形，可得AO = BO = CO = DO，AC ⊥ BD、又E，F，G，H分别是OA，OB，OC，OD的中点，可得EO = FO = GO = HO.

∴ 四边形EFGH是矩形.又EG ⊥ FH，

∴ 四边形EFGH是正方形.

18.2特殊的平行四边形同步学习（六）第四题答案

提示：作BF ⊥ DC，交DC的延长线于点F.

先证四边形BEDF是正方形，得BE = ED = DF = FB = 4.

再证△ABE ≌ △CBF，

∴ 四边形ABCD的面积等于正方形BEDF的面积16.

18.2特殊的平行四边形能力提升第一——四题答案

18.2特殊的平行四边形能力提升第五题答案

12

18.2特殊的平行四边形能力提升第六题答案

12

18.2特殊的平行四边形能力提升第七题答案

（1）提示：证明DE = DC，DF = DC

（2）当D为AC的中点时，四边形AECF为矩形、（理由略、）

18.2特殊的平行四边形能力提升第八题答案

提示：连接AC、由四边形ABCD为菱形，且∠B = 60°，

可得△ABC和△ACD为等边三角形，从而可证△ABE ≌ △ACF，

∴ AE = AF.又∠EAF = 60°，

∴ △AEF为等边三角形.

18.2特殊的平行四边形能力提升第九题答案

提示：连接PC.由正方形ABCD，可得△ABP ≌ △CBP，

∴ AP = CP.再证四边形PECF是矩形，

∴ PC = EF，

∴ AP = EF.

18.2特殊的平行四边形能力提升第十题答案

（1）MN = DM提示：在AD上取中点F，连接MF，证明△DFM ≌ △MBN，即可得DM = MN.

（2）MN = DM仍成立.提示：在AD上取一点P，使DP = MB，连接MP，证明△DPM ≌ △MBN即可.