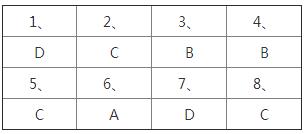
初中数学测试题一第一——八题答案
初中数学测试题一第九题答案
6
初中数学测试题一第十题答案
a(x+1)(x-2)
初中数学测试题一第十一题答案
≤4
初中数学测试题一第十二题答案
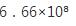
初中数学测试题一第十三题答案
1<x<2
初中数学测试题一第十四题答案
3/5
初中数学测试题一第十五题答案
4m
初中数学测试题一第十六题答案
2<x<2
初中数学测试题一第十六题答案
2<x<2
初中数学测试题一第十七题答案
x=5/2
初中数学测试题一第十八题答案
(1)15÷30%=50(人)
(2)50-(15+25)=10,10/50×360°=72°
(3)(5×15+10×25+15×10)×800/50=1600(元)
初中数学测试题一第十九题答案
BE⊥CE,BE=CE.理由如下:
∵△AED为等腰直角三角形,
∴AE=ED,∠EAD=∠EDA=45°,
∴∠EAB=90°+45°=135°=∠EDC,
又AC=2AB,点D是AC的中点,
∴AB=CD.
∴△BAE≌△CDE.
∴BE=CE,∠AEB=∠DEC,
∴∠AEB+∠BED=∠DEC+∠BED=90°
∴BE⊥CE.
初中数学测试题一第二十题答案
(1)(画树状图路);
(2)点Q落在直线y=x-3上的概率P=2/6=1/3
初中数学测试题一第二十一题答案
(1)第①种方法:y₁=4×2+5×(x-4)=5x+60; 第②种方法:y₂=(4×20+5x)×0.9=4.5x+72
(2)当y₁=y₂时,5x+60=4.5x+72,∴x=24;
当y₁>y₂时,5x+60>4.5x+72,∴x>24;
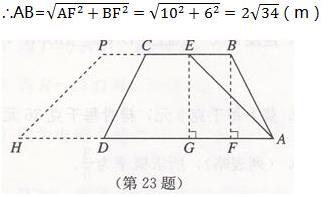
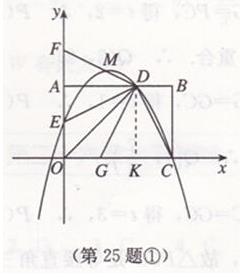
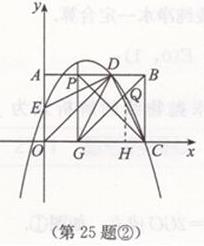
当y₁ 综上所述,当x=24时,两种方法一样便宜;当x>24时,第②种方法便宜;0<x<24时,第①种方法便宜。 初中数学测试题一第二十二题答案 (1)∵∠ACB=90°, ∴∠B=90°-∠A. ∵∠A=2∠DCB, ∴∠B=90°-2∠DCB. 如图,连接DO,则DO=CO. ∴∠DCB=∠ODC. ∴∠B=90°-2∠ODC而∠CDA=∠B+∠DCB=∠B+∠ODC, ∴∠CDA+∠ODC=∠B+2∠ODC=90°. ∴∠ODA=90° ∴AB是⊙O的切线。 (2)如图,作OF⊥CD,垂足为F,则OF=1,由BO=BE+OE=2OD知,∠DOB=60°. ∴∠ODF=(∠DOB)/2=30°. 在Rt△ODF中,有OD=OF/(sin30° )=2.故BO=4, 初中数学测试题一第二十三题答案 (1)如图:作EG⊥AD,垂足为G,BF⊥AD,垂足为F。 ∵BF/AF=5/3,BF=10, ∴AF=6. (2)如图,延长EC至点P,延长AD至点H,连接PH,由方案修改前后,修建大坝所需土石方的总体积不变,知S△ABE=S梯形CPHD。 ∴1/2 BE×EG= 1/2 (PC+HD)×EG即BE=PC+HD, ∴HD=BE-PC。 在Rt△AEG中,i=EG/AG=5/6,且EG=10, ∴AG=12,BE=GF=AG-AF=6, ∴HD=6-2.7=3.3(m)即坝底将会沿AD方向加宽3.3m。 初中数学测试题一第二十四题答案 (1)y=-80x+720. (2)当a=120时,购买饮料的支出是50×120=6000(元);当y=380时,x=17/4,饮桶装纯净水的支出是17/4×380+780=2395(元),∴购买饮料的方式花钱多。 (3)设饮桶装纯净水的支出为w元,则W=xy+780=x(-80x+720)+780=-80x2+720x+780. 若集体改饮某品牌的桶装纯净水一定合算,则2400≤50a. ∴a≥48. ∴当a至少为48元时,该班学生集体改饮某品牌的桶装纯净水一定合算。 初中数学测试题一第二十五题答案 (1)E(0,1) (2)所求抛物线的解析式为y=-5/6 x2+13/6 x+1 (3)EF=2GO 成立。如图①。 ∵点M在该抛物线上,且它的恨坐标为6/5, ∴点M的坐标为12/5。易得直线DM的解析式为y=-1/2 x+3 ∴F(0,3),EF=2. 过点D作DK⊥OC,垂足为K,则DA=DK, ∵∠ADK=∠FDG=90°, ∴∠FDA=∠GDK.又∠FAD=∠GKD=90°, ∴△DAF≌△DKG. ∴KG=AF=1. ∴GO=1. ∴EF=2GO. (4)∵点P在AB上,G(1,0)C(3,0),则设P(t,2). ∴PG2=(t-1)2+22,PC2=(3-t)2+22,GC=2. 如图② PG=PC,得t=2,∴P(2,2).此时点Q与点P重合。∴Q(2,2)。 若PG=GC,得t=1,∴P(1,2)。此时GP⊥x轴。∴Q(1,7/3) ③若PC=GC,得t=3, ∴P(3,2).此时PC=GC=2,故△PCG是等腰直角三角形, 过点Q作QH⊥x轴,垂足为H,则QH=GH,设QH=h, ∴Q(h+1,h). ∴-5/6(h+1)^2+13/6 (h+1)+1=h.解得h_1=7/5,h_2=-2(舍去)。 ∴Q(12/5,7/5). 综上所述,存在三个满足条件的点Q,即Q(2,2)或Q(1,7/3)或Q(12/5,7/5)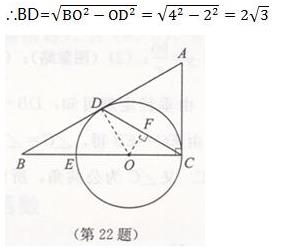

 九年级下册英语同步解析与测评答案人教版
九年级下册英语同步解析与测评答案人教版 九年级下册物理同步解析与测评答案人教版
九年级下册物理同步解析与测评答案人教版 九年级下册化学同步解析与测评答案人教版
九年级下册化学同步解析与测评答案人教版 九年级下册历史同步解析与测评答案人教版
九年级下册历史同步解析与测评答案人教版 九年级下册数学同步解析与测评答案人教版
九年级下册数学同步解析与测评答案人教版 鲁教版语文书九年级下册答案
鲁教版语文书九年级下册答案 北师大版数学书九年级下册答案
北师大版数学书九年级下册答案 人教版语文书九年级下册答案五四制
人教版语文书九年级下册答案五四制 华东师大版数学书九年级下册答案
华东师大版数学书九年级下册答案 苏科版数学书九年级下册答案
苏科版数学书九年级下册答案 湘教版数学书九年级下册答案
湘教版数学书九年级下册答案 鲁教版数学书九年级下册答案五四制
鲁教版数学书九年级下册答案五四制 译林版英语书九年级下册答案
译林版英语书九年级下册答案 沪教版英语书九年级下册答案
沪教版英语书九年级下册答案 外研版英语书九年级下册答案
外研版英语书九年级下册答案 九年级下册数学课时作业本答案人教版
九年级下册数学课时作业本答案人教版 九年级上册思想品德学法大视野答案人教版
九年级上册思想品德学法大视野答案人教版 九年级思想品德新编基础训练答案人教版
九年级思想品德新编基础训练答案人教版 九年级上册语文同步练习答案苏教版
九年级上册语文同步练习答案苏教版 九年级下册数学作业本答案浙教版
九年级下册数学作业本答案浙教版 九年级下册化学课时练答案人教版
九年级下册化学课时练答案人教版 九年级下册英语同步训练答案人教版
九年级下册英语同步训练答案人教版 九年级上册数学同步解析与测评答案人教版
九年级上册数学同步解析与测评答案人教版 人教版九年级下册语文南方新课堂答案
人教版九年级下册语文南方新课堂答案