巩固基础、提升能力、综合创新第8题答案
DC= EB
或CF=BF
或DF=EF
或F为DE的中点
或F为BC的中点
或AB=BE
或B为AE的中点
巩固基础、提升能力、综合创新第9题答案
65°
巩固基础、提升能力、综合创新第10题答案
（1）证明：在▱ABCD中，AB∥CD，AB=CD
∵AE=CF，
∴BE=DF，且BE∥DF
∴四边形BFDE是平行四边形
∴DE=BF
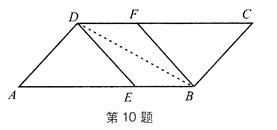
（2）解：连接BD，如上图，图中有三对全等三角形：
△ADE≌△CBF，△BDP-≌△DBF，△ABD≌△CDB
巩固基础、提升能力、综合创新第11题答案
证明：△AB'C是由△ABC沿AC对折得到的图形，
∴∠BAC=∠B'AC，
∵在▱ABCD中，AB∥CD，
∴∠BAC=∠DCA，
∴∠DCA=DB'AC，
∴OA=OC
巩固基础、提升能力、综合创新第12题答案
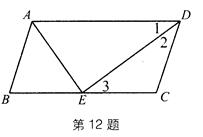
（1）证明：如图，在▱ABCD中，
由，AD∥BC得∠1=∠3，
又∵∠1=∠2．
∴∠2=∠3，
∴CD=CE
（2）解：由▱ABCD得AB=CD，
又∵CD=CE ，BF=CE，
∴AB=BE，
∴∠BAE=∠BEA.
∵∠B=80°，
∴∠BAE=50°，∠DAE=180°- 50°- 80°= 50°
巩固基础、提升能力、综合创新第13题答案
证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AB=CD，AD=BC，
∴∠AEB=∠EBC
又∵BE平分∠ABC，
∴ ∠ABE=∠EBC，
∴∠ABE=∠AEB，
∴AB=AE.同理可得DC=DF
∴AE=DF，
∴AE - EF=DF -EF，即AF=DE
八年级下册英语同步训练答案人教版
八年级下册历史同步训练答案人教版
八年级下册语文同步训练答案人教版
八年级下册物理同步训练答案人教版
八年级下册思想品德同步训练答案人教版
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
浙教版八年级上册科学课时特训答案
英语八年级上册学习与评价答案译林版
八年级上册生物学法大视野答案苏教版
八年级下册历史同步解析与测评答案人教版
八年级下册地理课时练答案人教版
八年级下册语文作业本答案人教版
八年级下册思想品德同步精练答案粤教版
八年级下册生物长江全能学案同步练习册答案人教版