巩固基础、提升能力、综合创新第8题答案
证明：∵b>0，
∴a2+b2>a2-b2，
∵a>b，
∴（a-b）2>0，，
∴a2+b2>2ab，即a2+b2为三边中最长边．
∵（a2+b2）2=a⁴+2a2b2+ b⁴，
（a2-b2）2+（2ab）2= a⁴-2a2b2+b⁴+4a2b2= a⁴+ 2a2b2+b⁴，
即（a2-b2）2+（2ab）2=（a2+ b2）2，
∴三条边长分别为a2-b2，2ab，a2+b2（a>b）的△ABC是直角三角形
巩固基础、提升能力、综合创新第9题答案
C
巩固基础、提升能力、综合创新第10题答案
解：连接AC，
∵∠B =90°，AB =4，BC =3，
在Rt△ABC中，根据勾股定理得AC2= AB2+ BC2= 32 +42=52，
∴AC=5．
在△ACD中，AC =5，AD=12，CD=13，
AC2+AD2=52+122= 169，
CD2= 132= 169，即AC2+ AD2= CD2，
∴△ACD是直角三角形
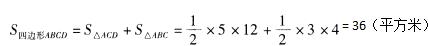
答：四边形ABCD的面积是36平方米
巩固基础、提升能力、综合创新第11题答案
解：6分钟=1/10小时，AC=120×1/10=12（海里），
BC=50×1/10=5（海里）
∵AB=13海里，
∴在△ABC中，AC2+ BC2= AB2，即∠C=90°，
∵∠CBA=50°，
∴∠CAB=40°，
∴甲船航向为北偏东50°
巩固基础、提升能力、综合创新第12题答案
解：（1）直角三角形．
∵DB=90°，AB=BC=4，
∴AC2= AB2+ BC2= 42+ 42= 32，
AD2=22 =4，CD2= 62=36，，
∴AC2+AD2= CD2，
∴△ACD是直角三角形．
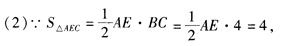
∴AE=2，
∴BE=2，
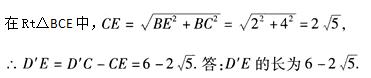
八年级下册英语同步训练答案人教版
八年级下册历史同步训练答案人教版
八年级下册语文同步训练答案人教版
八年级下册物理同步训练答案人教版
八年级下册思想品德同步训练答案人教版
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
八年级上册物理学法大视野答案人教版
八年级下册物理同步导学与优化训练答案人教版
外研版八年级上册英语课时特训答案
人教版八年级上册英语课时特训答案
人教版八年级上册语文课时特训答案
八年级下册语文课时特训答案人教版
八年级下册数学书答案青岛版
八年级下册英语长江全能学案阅读训练答案人教版
八年级下册生物长江全能学案同步练习册答案人教版