巩固基础、提升能力、综合创新第11~12题答案
C；C
巩固基础、提升能力、综合创新第13题答案
（ 1）证明 :∵ AC平分 ∠ DAB ,
∴∠DAC = ∠CAB,
∵ ∠ADC = ∠ACB = 90°，
∴△ADC∽△ACB,
∴ AD: AC =AC: AB,
∴ AC2= AB .AD．
（2）证明：∵E为AB的中点，
∴CE=EB=AE，
∴∠EAC=∠ECA,
∵∠DAC=∠CAB，
∴∠DAC=∠ECA，
∴CE∥AD.
（3）解：∵CE∥AD
∴△AFD∽△CFE,
∴AD: CE =AF: CF
∵CE=（1/2）4B=1/2×6 =3,AD =4，
∴4/3=AF/CF，
∴AC/AF=7/4
巩固基础、提升能力、综合创新第14题答案
（1）图略
（2）证明：∵DE垂直平分AB，
∴DA=DB, ∠ABD=∠BAC,
∵∠ABC=80°,∠BAC=40°,
∴ ∠ABD=∠BAC=40°，
∴∠CBD=40°= ∠BAC，
又∵∠ACB=∠DCB,
∴△ABC∽△BDC
巩固基础、提升能力、综合创新第15题答案
（1）证明：∵四边形ABCD是平行四边形，
∴AB∥CD,AD∥BC，
∴∠C+∠B=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C
在△ADF与△DEC中，
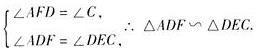
（2）解：∵四边形ABCD是平行四边形，
∴CD=AB=8，
由（1）知△ADF∽△DEC，
∴AD/DE=AF/CD，
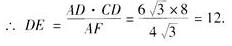
在Rt△ADE中，由勾股定理得
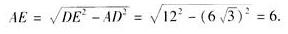
巩固基础、提升能力、综合创新第16题答案
（1）不相似，
∵在Rt△ABC中，∠A=90°，AB=3，AC=4，
在Rt△DEF中，∠D=90°，DE=3，DF=2，
∴Rt△ABC与Rt△DEF不相似
（2）能作
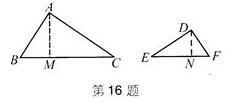
如图所示的辅助线进行分割．
具体作法：作∠BAM=∠E，交BC于M；
作∠NDE=∠B，交EF于N，
由作法和已知条件可知△BAM≌△DEN
∵ BAM=∠E.∠NDE=∠B,∠AMC=∠BAM+∠B,∠FND=∠E+∠NDE,
∴ ∠AMC=∠FND
∵∠FDN = 90°-∠NDE,∠C= 90°-∠B,
∴∠FDN=∠C.
∴△AMC≌△FND
巩固基础、提升能力、综合创新第17题答案
解 :如图，作NH⊥AC于H，易证△ANH∽△ABC，
九年级下册语文同步训练答案人教版
九年级下册英语同步训练答案人教版
九年级下册数学同步训练答案人教版
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
物理九年级下册学习与评价答案苏科版
九年级下册科学作业本答案浙教版
九年级下册数学新编基础训练答案人教版
九年级上册物理配套练习册答案人教版
九年级下册语文书答案人教版
北师大版九年级上册数学书答案
人教版九年级上册语文作业本答案
北师大版九年级下册数学作业本答案江西省
九年级上册语文同步练习答案苏教版
苏人版九年级上册思想品德伴你学答案