巩固基础、提升能力、综合创新第16题答案
∠1=65°
巩固基础、提升能力、综合创新第17题答案
C
巩固基础、提升能力、综合创新第18题答案
40°
巩固基础、提升能力、综合创新第19题答案
30°
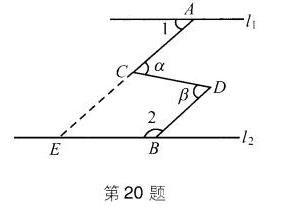
巩固基础、提升能力、综合创新第20题答案
解：延长AC交直线l2于点E
∵l1//l2，
∴∠AEB=∠1=40°
又∵∠α=∠β，
∴AE//DB
∴∠2+∠AEB=180°
∴∠2==180° - ∠AEB=180° - 40°= 140°
巩固基础、提升能力、综合创新第21题答案
由图1，可得∠PAB+∠PCD=360° - ∠APC；
由图2，可得∠APC=∠PAB+∠PCD；
由图3，可得∠APC=∠PCD -∠PAB；
由图4，可得∠APC=∠PAB - ∠PCD
如图3，AB//CD.说明∠APC=∠PCD - ∠PAB的理由，
说明：∵AB//CD，
∴∠PCD+∠CEB=180°（两直线平行，同旁内角互补）
又∵∠PAB+∠APC+∠AEP=180°（三角形的内角和等于180°，
∠AEP=∠CEB（对顶角相等），
∴∠PAB+∠APC+∠CEB=180°
∴∠PAB+ ∠APC+∠CEB=∠PCD+∠CEB（等量代换）
∴∠APC=∠PCD - ∠PAB
七年级下册地理同步训练答案人教版
七年级下册语文同步训练答案人教版
七年级下册数学同步训练答案人教版
七年级下册历史同步训练答案冀人版
苏科版七年级下册数学书答案
北师大版七年级下册数学书答案
语文版七年级下册语文课本答案
浙教版七年级下册科学课本答案
浙教版七年级下册数学课本答案
北师大版七年级下册生物课本答案
北师大版七年级下册历史课本答案
北师大版七年级下册语文课本答案
苏教版七年级下册语文课本答案
七年级下册数学书答案人教版
七年级下册历史南方新课堂答案人教版
七年级下册地理同步导学与优化训练答案人教版
北师大版七年级上册数学书答案
人教版七年级上册语文作业本答案江西省
浙教版七年级上册数学作业本答案
七年级下册语文课时练答案人教版
七年级下册英语课时练答案人教版
人教版七年级下册生物作业本答案江西省
七年级下册思想品德新编基础训练答案粤教版
七年级下册生物同步精练答案北师大版