基础练习24.6（二）第1~3题答案
| 1 | 2 | 3 |
| B | D | A |
基础练习24.6（二）第4题答案
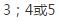
基础练习24.6（二）第5题答案
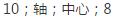
基础练习24.6（二）第6题答案
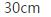
基础练习24.6（二）第7题答案
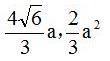
基础练习24.6（二）第8题答案
证明，如图，连接OM,ON, MN垂直平分OB，
∴OM=MB，
∵OM=OB，
∴△OBM为等边三角形，
∴∠MOB=60°,即360°/n1=60°，
∴MB为正六边形的一个边。
AB⊥CD，
∴∠COM=90°-60°=30°，即360°/n2=30°
∴n2=12
所以CM为正十二边形的一个边，
同理，由∠COB=90°,得CB正四边形的一个边，∠MON=120°,得MN为正三角形的一个边
连接OM,ON 易证
基础练习24.6（二）第9题答案
略
推荐阅读
九年级下册化学同步练习答案沪教版
年级：九年级
版本：上教版
科目：化学
学期：下册
名称：同步练习
九年级下册数学同步练习答案沪科版
年级：九年级
版本：沪科版
科目：数学
学期：下册
名称：同步练习
九年级下册数学同步练习答案苏科版
年级：九年级
版本：苏科版
科目：数学
学期：下册
名称：同步练习
九年级下册英语同步练习答案译林版
年级：九年级
版本：译林版
科目：英语
学期：下册
名称：同步练习
九年级下册语文同步练习答案苏教版
年级：九年级
版本：苏教版
科目：语文
学期：下册
名称：同步练习
鲁教版语文书九年级下册答案
年级：九年级
版本：鲁教版
科目：语文
学期：下册
名称：课本
北师大版数学书九年级下册答案
年级：九年级
版本：北师大版
科目：数学
学期：下册
名称：课本
人教版语文书九年级下册答案五四制
年级：九年级
版本：人教版
科目：语文
学期：下册
名称：课本
华东师大版数学书九年级下册答案
年级：九年级
版本：华东师大版
科目：数学
学期：下册
名称：课本
苏科版数学书九年级下册答案
年级：九年级
版本：苏科版
科目：数学
学期：下册
名称：课本
湘教版数学书九年级下册答案
年级：九年级
版本：湘教版
科目：数学
学期：下册
名称：课本
鲁教版数学书九年级下册答案五四制
年级：九年级
版本：鲁教版
科目：数学
学期：下册
名称：课本
译林版英语书九年级下册答案
年级：九年级
版本：译林版
科目：英语
学期：下册
名称：课本
沪教版英语书九年级下册答案
年级：九年级
版本：沪教版
科目：英语
学期：下册
名称：课本
外研版英语书九年级下册答案
年级：九年级
版本：外研版
科目：英语
学期：下册
名称：课本
人教版九年级上册数学新课程自主学习与测评答案
年级：九年级
版本：人教版
科目：数学
学期：上册
名称：新课程自主学习与测评
人教版九年级上册语文书答案
年级：九年级
版本：人教版
科目：语文
学期：上册
名称：课本
人教版九年级下册语文作业本答案江西省
年级：九年级
版本：人教版
科目：语文
学期：下册
名称：作业本
九年级下册数学课课练答案苏科版
年级：九年级
版本：苏科版
科目：数学
学期：下册
名称：课课练
北师大版九年级下册数学作业本答案江西省
年级：九年级
版本：北师大版
科目：数学
学期：下册
名称：作业本
九年级下册语文长江作业本答案鄂教版
年级：九年级
版本：鄂教版
科目：语文
学期：下册
名称：长江作业本
浙教版九年级上册科学书答案
年级：九年级
版本：浙教版
科目：科学
学期：上册
名称：课本
九年级下册英语课时特训答案人教版
年级：九年级
版本：人教版
科目：英语
学期：下册
名称：课时特训
鲁教版数学书九年级下册答案五四制
年级：九年级
版本：鲁教版
科目：数学
学期：下册
名称：课本
九年级下册物理课时作业本答案人教版
年级：九年级
版本：人教版
科目：物理
学期：下册
名称：课时作业本