角的平分线性质（二）第1题答案
提示：作两个角的平分线，交点即为建加油站的位置。
角的平分线性质（二）第2题答案
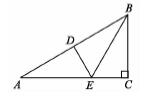
证明：∵D是AB的中点，
∴BD=AB
∵AB=2BC
∴BC=AB
∴BD=BC
又∵DE⊥AB，∠C=90°
∴∠C=∠BDE=90°
又BE=BE，
∴Rt∆BDE≌Rt∆BCE（HL）
∴∠DBE=∠CBE
∴BE平分∠ABC
角的平分线性质（二）第3题答案
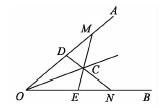
提示：作CE⊥OA于E，CF⊥OB于F，OM=ON，OE=OD，∠MOE=∠NOD
∴∆MOE≌∆NOD（SAS）
∴S∆MOE=S∆NOD，同时去掉S四边形ODCE，得S∆MDC=S∆NEC，易证，MD=NE，
∴CE=CF，
∴点C在∠AOB的平分线上
角的平分线性质（二）第4题答案
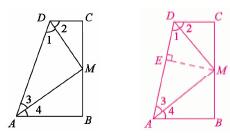
（1）AM平分∠BAD
证明：过点M作ME⊥AD，垂足为E
∵∠1=∠2，MC⊥CD，ME⊥AD
∴ME=MC
又∵MC=MB，∴ME=MB
∵MB⊥AB，ME⊥AD
∴AM平分∠BAD
（2）AM⊥DM
理由如下：
∵∠B=∠C=90°
∴CD∥AB
∴∠CDA+∠DAB=180°
又∵∠1=∠CDA，∠3=∠DAB
∴2∠1+2∠3=180°
∴∠1+∠3=90°
∴∠AMD=90°，即AM⊥DM
人教版八年级上册数学作业本答案江西省
北师大版八年级上册数学作业本答案江西省
人教版八年级上册英语作业本答案江西省
沪粤版八年级上册物理作业本答案江西省
教科版八年级上册物理作业本答案江西省
八年级上册物理书答案人教版
华东师大版八年级上册数学书答案
青岛版八年级上册数学书答案
人教版八年级上册英语书答案
浙教版八年级上册科学书答案
浙教版八年级上册数学书答案
人教版八年级上册语文书答案
沪科版八年级上册数学书答案
北师大版八年级上册数学书答案
人教版八年级上册数学书答案
人教版八年级下册英语作业本答案江西省
八年级上册语文新编基础训练答案人教版
八年级下册物理课时练答案人教版
八年级下册思想品德新编基础训练答案人教版
八年级下册语文配套练习册答案人教版
人教版八年级下册数学配套练习册答案
八年级下册语文同步训练答案人教版
八年级下册语文南方新课堂答案人教版
八年级下册历史新课程自主学习与测评答案人教版