课时达标第1~3题答案
| 1 | 2 | 3 |
| D | C | C |
课时达标第4题答案
平行四边形
课时达标第5题答案
B
能力展示第1题答案
∵四边形ABCD为平行四边形，
∴AB=CD, AB∥CD
又∵EC∥BD，
∴四边形BECD为平行四边形，
∴BE=CD
∴BE =AB
能力展示第2题答案
DE∥AC，DF∥AB，
∴四边形AEDF为平行四边形．
∴AE=DF
∵AB=AC
∴∠B=∠C
∵DE∥AC
∴∠BDE=∠C,
∴∠B=∠BDE,
∴BE=DE，
∴DE+DF=BE +AE=AB
能力展示第3题答案
∵E，F，G，日分别是AB, OC, CD, OA的中点，
∴EH, FG分另4是△ABO和△COD的中位线，
∴EH=1/2OB，EH∥OB, FC=1/2OD, FC∥OD
∴EH//FG
∵四边形ABCD为平行四边形，
∴OB=OD，
∴EH=FG
∴四边形EFGH为平行四边形
尝试提高第1题答案
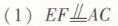
（2）在△ABC中，∵AE=BE，CD=BD，
∴DE∥AC，DE=1/2AC
∴EF∥AC
又∵GF∥AD
∴四边形ADFG是平行四边形，
∴FD =AG
又∵AG=1/2AC，
∴DE =AG
∴EF=DE+ DF=AG +AG =2AG =AC
尝试提高第2题答案
可以，如四边形AP₁CP₇、四边形AP₂CP₆、四边形AP₃ CP₅都是平行四边形，
以四边形AP₁CP₇为例，理由如下：
∵四边形ABCD为平行四边形，
∴AB=CD, AB∥CD.
∴∠ABP₁=∠CDP₇.
又∵BP₁=DP₇，
∴△ABP₁≅△CDP₇.
∴AP₁=CP₇, ∠AP₁B=∠CP₇D.
∴∠AP₁D=∠CP₇B.
∴AP₁∥CP₁
∴四边形AP₁CP₁是平行四边形
人教版八年级下册物理南方新课堂答案
八年级下册数学南方新课堂答案人教版
八年级下册地理南方新课堂答案人教版
八年级下册历史南方新课堂答案人教版
八年级下册语文南方新课堂答案人教版
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
八年级下册生物伴你学答案苏科版
八年级下册思想品德作业本答案人教版
八年级上册数学人教版长江全能学案答案
八年级下册数学书答案沪科版
人教版八年级上册英语书答案
八年级下册物理课课练答案苏科版
八年级下册物理长江全能学案同步练习册答案人教版
八年级下册生物课时练答案人教版
人教版八年级下册语文知识与能力训练答案