课后作业第6~7题答案
B；B
课后作业第8题答案
24
课后作业第9题答案
2
课后作业第10题答案
(1)连接CM
∵∠PAC=∠ABC，∠M=∠ABC，
∴∠PAC=∠M
∵AM是⊙O的直径，∴∠ACM= 90°．
∴∠M+∠MAC= 90°
∴∠PAC+ ∠MAC=90°，
即∠MAP=90°
∴MA⊥PA
∴PA是⊙O的切线
(2)连接AE.
∵AM⊥AP，∴AP//BC
∴∠P= ∠CBD.
∵∠PDA=∠BDC，△CDB∽△ADP．BD/PD=CD/AD.
∠CBD=∠CAE，
∴∠P= ∠CAE
∵∠P=∠DCF，
∴∠DCF=∠CAE
∵∠ADE=∠CDF，
∴△CDF ∽△ADE.
∴CD/AD=FD/ED
∴BD/PD=FD/ED=CD/AD
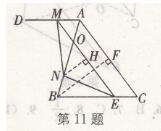
课后作业第11题答案
(1)∵AD//BC，ME//AC，
∴四边形AMEC是平行四边形，
∴AC=ME=6 ,AM=EC=x.
∵AD//BC，
∴∠MAO= ∠EBO.
∵∠AOM=∠BOE
∴△AOM∽△BOE
∴AM/BE=MO/OE，即x/5-x=MO/6-MO
∴MO=6/5x
(2)如图，作BF⊥AC, NH⊥ ME，垂足分别为F.H，则易得AF=CF=3，BF=4
∵AB=BC=5
∴∠BAC= ∠BCA
又∵∠AME=∠BCA，∠ AOM=∠BAC，
∴∠AME=∠AOM
∴AM=AO=x
∴当0<x<号时，ON=5-2x,
∵∠OHN=∠AFB=90°,
∠NOH=∠BAF,
∴△OHN∽△AFB，
∴NH/BF=ON/AB
∴NH/4=5-2x/5
∴NH=-8/5x+4
∴y=1/2MO•NH=1/2×6/5x×（-8/5x+4）=-24/25x2+12/5x．
自变量x的取值范围是0<x<号
(3)点拨：如图，由AM= BN=x，AN=BE=5-x,∠MAN=∠NBE，
得△MAN≌△NBE. ∴MN= NE
∵∠NMO=∠EMN.
∴若△MNE 与△MON相似，只有△MNE∽△MON，可得OM= ON.
∴6/5x=5 – 2x，解得x=25/16
∴若△MNE与△M0N相似．AM的长为25/16．
九年级下册语文课时作业本答案人教版
九年级下册数学课时作业本答案人教版
九年级下册化学课时作业本答案人教版
九年级下册物理课时作业本答案人教版
九年级下册英语课时作业本答案人教版
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
九年级下册语文长江作业本答案鄂教版
九年级下册数学配套练习册答案青岛版
九年级下册数学新编基础训练答案人教版
浙教版九年级上册科学课时特训答案
九年级下册思想品德作业本答案人教版
九年级下册数学书答案华东师大版
英语九年级上册学习与评价答案译林版
九年级上册物理同步解析与测评答案人教版
九年级上册数学配套练习册答案人教版