课后作业第9题答案
180°
课后作业第10题答案
133°
课后作业第11题答案
∵ ∠A=∠D，
∴AB//CD(内错角相等，两直线平行)
∴∠ABC= ∠BCD（两直线平行，内错角相等）
∵ BE平分∠ABC，CF平分∠BCD，
∴∠1=1/2ABC，
∠2=1/2∠BCD
∴∠1=∠2
∴BE//CF（内错角相等，两直线平行）
∴∠3=∠4（两直线平行，内错角相等）
∴∠AEB=∠CFD（等角的补角相等）
课后作业第12题答案
∠AED=∠C
∵ ∠1+∠2=∠80°，∠1+∠DFE=180°（邻补角的定义），
∴ ∠2=∠DFE
∴AB//EF（内错角相等，两直线平行）
∴∠ADE= ∠3（两直线平行，内错角相等）
又∵ ∠3=∠B，
∴∠B=∠ADE
∴DE//BC（同位角相等，两直线 平行）
∴∠AED=∠C（两直线平行，同位角相等）
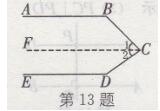
课后作业第13题答案
(1)如图，过点C向左画CF//B，CF把∠BCD分为∠1和∠2，
则∠1+∠B=180°（两直线平行，同旁内角互补），
∴∠1=180°-∠B=45°
∵CF//AB， DE//AB，
∴CF//DE
（如果两条直线都与第三条直线平行，那么这两条直线也互相平行）
同理可得 ∠2=180°=∠D=35°
∴∠BCD=∠1+∠2=45°+35°=80°
(2)∠B+∠BCD+∠D=360°
理由：如图，过点C向左画CF//AB，
CF把∠BCD分为∠1和 ∠2，
则∠B+∠1=180°（两直线平行，同旁内角互补）
∵ CF//AB，DE//AB，
∴CF//DE
(如果两条直线都与第三条直线平行，那么这两条直线也互相平行）
同理可得∠D+ ∠2=180°，
∴∠B+∠1+∠2+ ∠D=360°，
即∠B+∠BCD+∠D=360°
(3)∠B+∠C+∠D+∠E= 540°
七年级下册数学课时作业本答案人教版
七年级下册英语课时作业本答案人教版
七年级下册语文课时作业本答案人教版
苏科版七年级下册数学书答案
北师大版七年级下册数学书答案
语文版七年级下册语文课本答案
浙教版七年级下册科学课本答案
浙教版七年级下册数学课本答案
北师大版七年级下册生物课本答案
北师大版七年级下册历史课本答案
北师大版七年级下册语文课本答案
苏教版七年级下册语文课本答案
七年级下册数学书答案人教版
七年级下册语文课时特训答案人教版
七年级下册数学作业本答案浙教版
七年级上册历史学法大视野答案岳麓版
人教版七年级上册语文新课程自主学习与测评答案
七年级下册历史长江全能学案同步练习册答案人教版
七年级下册语文新课程自主学习与测评答案人教版
人教版七年级上册数学课时练答案
七年级上册语文配套练习册答案人教版
七年级下册语文新编基础训练答案人教版