反比例函数第3课时第1题答案
y=2/x（x≠0）
反比例函数第3课时第2题答案
5 2 （-5/3，-3）
反比例函数第3课时第3~5题答案
| 3 | 4 | 5 |
| D | C | A |
反比例函数第3课时第6题答案
解：（1）∵双曲线y=4/x的图像位于一、三象限，直线y=x的图像位于一、三象限
∴双曲线y=4/x与y=x的位置关系是相交的，双曲线y=4/x关于y=x对称
（2）双曲线y=4/x在一、三象限，y=-x在二、四象限，它们没有交点，但y=4/x关于y=-x对称
反比例函数第3课时第7题答案
解：（1）把（2，-1）代入y₁=k/x，解得k=-2，
∴y₁=-2/x（x≠0），把（2，-1）代入y₂=-mx+3，解得m=2，∴k=-2，m=2
（2）由（1）得y₁=-2/x，y₂=-2x+3，
令y₁=y₂得另一个交点为（-1/2,4），
令y₁>y₂得x>2，令y₁<y₂得0<x<2或x<-1/2
反比例函数第3课时第8题答案
解：（1）由题意得：
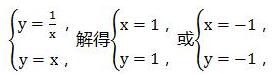
∴A（1，1）C（-1，-1）
∵AB⊥x轴，CD⊥x轴
∴B（1，0） D（-1，0）
（2）由（1）可知：A（1，1）C（-1，-1）B（1，0） D（-1，0）
∴BD=2，AB=CD=1
∵AB⊥BD CD⊥BD
∴BD∥CD
∴四边形ABCD为平行四边形，
∴S四边形ABCD=AB•BD=1×2=2
反比例函数第3课时第9题答案
解：根据等腰直角三角形的性质可知：P₁（a，a），
∴y=4/x，解得a=±2，又a>0，故a=2，
∴P₁（2，2），再根据等腰三角形三线合一性质可知：A₁的坐标为（4,0），
设点P₂的坐标为（4+b，b），又y=4/x
∴b2+4b-4=0且b>0
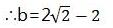
由等腰三角形三线合一性质得
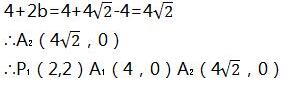
人教版九年级下册化学配套练习册答案
人教版九年级下册物理配套练习册答案
九年级下册数学配套练习册答案人教版
九年级下册数学配套练习册答案青岛版
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
九年级下册数学同步解析与测评答案人教版
九年级上册思想品德课课练答案苏人版
九年级下册数学书答案青岛版
苏科版九年级下册数学书答案
九年级上册语文学法大视野答案人教版
人教版九年级上册数学书答案
人教版九年级上册语文新课程自主学习与测评答案
九年级下册数学作业本答案浙教版
九年级下册化学同步解析与测评答案人教版