第1课时选择题答案
| 1 | 2 | 3 | 4 |
| D | A | C | D |
第1课时第5题答案
3
第1课时第6题答案
相似三角形为：△EAB∽△EDF∽△BCF
证明如下：
∵AD=2DE，∴AE=3DE，
∴DE/AE=1：3
∵AE和DE为相似三角形△EAB和△EDF的对应边，
∴△EAB是△EDF的三倍，
由此得：BE=3EF，
∴BF=2EF
BF和EF为相似三角形△BCF和△EDF的对应边，
∴△BCF是△EDF的二倍
∴△EAB、△EDF、△BCF的相似比为3：1：2
第1课时第7题答案
B
第1课时第8题答案
解：（1）∵DE∥BC，
∴△ADE∽△ABC
∵AD/AB=AE/AC =DE/BC，
∴AD/AB=4/（4+8）=AE/AC=1/3，
（2）∵DE/BC=AD/AB=3/BC=4/（4+8），
∴BC=9
第1课时第9题答案
证明：
∵AP=PQ=QD=BR=RS=SC，PQ∥BR，QD∥BC
∴四边形PBRQ和四边形QRSD都是平行四边形
∴DS∥QR∥PB
∵AK：KL：LM=AP：PQ：QD=1：1：1
∴AK=KL=LM
∵LM：MC=RS：SC=1：1
∴LM=MC
∴AK=KL=LM=MC
第1课时第10题答案
解：∵AE∥BD
∴△ECA∽△DCB
∴BC/AC=CD/EC
∵EC=8.7m，ED=2.7m，
∴CD=6m
∵AB=1.8m
∴AC=BC+1.8m
∴BC/（BC+1.8）=6/8.7
∴BC=4
即窗口底边离地面的高为4m
第1课时第11题答案
解：连接PP′交BC于O点，
∵若四边形PQCP′为菱形，
∴PP′⊥QC
∴∠POQ=90°
∵∠ACB=90°
∴PO∥AC
∴AP/AB=CO/CB
∵设点Q运动的时间为t秒
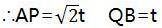
∴AP=√2t QB=t
∴QC=6-t
∴CO=3-t/2
∵AC=CB=6，∠ACB=90°
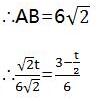
∴t=2
人教版九年级下册化学配套练习册答案
人教版九年级下册物理配套练习册答案
九年级下册数学配套练习册答案人教版
九年级下册数学配套练习册答案青岛版
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
九年级上册思想品德学法大视野答案人教版
人教版九年级下册历史知识与能力训练答案
九年级下册数学补充习题答案苏科版
九年级下册英语同步训练答案人教版
沪粤版物理书九年级下册答案
上教版九年级下册英语知识与能力训练答案
九年级下册化学书答案鲁教版
语文九年级上册学习与评价答案苏教版
教科版九年级下册物理作业本答案江西省