第2课时第1题答案
y = 2x2+x-2 向上 x = -1/4 （-1/4 ，-17/8）
第2课时第2题答案
y = -x2-2x+3
第2课时第3题答案
y = -1/2x2+ 1/2x+1
第2课时第4题答案
（1）将A、B、C坐标代入，可得a=-1，b=1，c=2，函数解析式为y=-x2+x+2
（2）对称轴为x=1/2，顶点坐标为（1/2 ，9/4）
第2课时第5题答案
（1）（1，1），（2，0）代入直线方程，解得 k=-1 b=2，则直线为y=-x+2 因为C（1，1），则代入
得 a=1，抛物线为 y=x2
（2）将两个方程联立得B（-2，4）
又因为O（0，0） C（1，1）
所以S△OBC=S△AOB-S△AOC=
1/2×[2-（-2）]×4-1/2×2×1
=4-3=3
因为S△OAD=S△OBC=3，且A（2，0） 所以设D（x，x2）
第2课时第6题答案
解：（1）因为抛物线与y轴交于正半轴，且OA=OB，
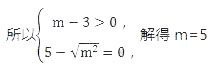
（2）抛物线的表达式为y=-1/2 x2+2，对称轴是y，顶点C的坐标是（0，2）；
（3）令y=0，得-1/2 x2+2=0，解得x=±2，
故A、B两点的坐标分别为A（2，0）B（-2，0），则△OAC是等腰直角三角形。
假设存在一点M，使△MAC≌△OAC，
因为AC是公共边，OA=OC，点M与点O关于直线AC对称，
则四边形OAMC是正方形，
所以M点的坐标为（2，2）
当x=2时，y=-1/2×22+2=0≠2，
所以点M（2，2）不在抛物线上，
即不存在M点是的△MAC≌△OAC
九年级上册物理配套练习册答案人教版
九年级上册数学配套练习册答案青岛版
九年级上册语文配套练习册答案人教版
九年级上册化学配套练习册答案人教版
九年级上册数学配套练习册答案人教版
九年级上册化学课本答案沪教版
华东师大版九年级上册数学书答案
人教版九年级上册化学书答案
人教版九年级上册物理书答案
人教版九年级上册英语书答案
浙教版九年级上册科学书答案
沪科版九年级上册数学书答案
浙教版九年级上册数学书答案
人教版九年级上册语文书答案
北师大版九年级上册数学书答案
九年级下册数学同步解析与测评答案人教版
九年级下册数学书答案青岛版
九年级下册物理长江作业本答案人教版
九年级下册数学课时作业本答案人教版
人教版九年级上册思想品德作业本答案
人教版九年级下册语文知识与能力训练答案
九年级下册化学课本答案人教版
人教版九年级下册历史知识与能力训练答案
九年级下册数学书答案华东师大版