第十二章综合练习第13题答案
有相等的角，分别是：∠BAC=∠BAD，∠CBA=∠DBA，∠C=∠D，∠CBE=∠DBE
理由如下： ∵AC=AD，BC=BD，AB为公共边，
∴△ABD≌△ABC，
∴∠BAC=∠BAD，∠CBA=∠DBA，∠C=∠D，∠CBE=∠DBE
第十二章综合练习第14题答案
证明：∵M是AB的中点，
∴AM=BM，
又∵MC=MD，∠CMA=∠DMB，
∴△AMC≌△BMD（SAS），
∴AC=BD
第十二章综合练习第15题答案
证明：
因为AB平行DE
所以∠ABC=∠DEF（两直线平行，同位∠相等）
因为BE=CF，CE=CE
所以BE+CE=CF+CE
所以BC=EF（等式的性质）
在△ABC和△DEF中
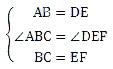
所以△ABC全等于△DEF（SAS）
所以∠ACB=∠DFE（全等三角形对∠相等）
所以AC平行DF（同位∠相等，两直线平行）
第十二章综合练习第16题答案
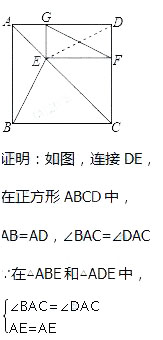
∴△ABE≌△ADE（SAS），
∴BE=DE，
∵EF⊥CD于F，EG⊥AD于G，∠ADC=90°，
∴四边形EFDG是矩形，
∴DE=FG，
∴BE=FG
第十二章综合练习第17题答案
解：（1）五个结论：OB=OC；OA=BD；
∠ABO=∠DCO；∠ABC=∠DCB
（2）选证：OB=OC。
第十二章综合练习第18题答案
八年级上册物理配套练习册答案人教版
八年级上册语文配套练习册答案人教版
八年级上册物理配套练习册答案沪科版
八年级上册英语配套练习册答案人教版
八年级上册数学配套练习册答案青岛版
八年级上册物理书答案人教版
华东师大版八年级上册数学书答案
青岛版八年级上册数学书答案
人教版八年级上册英语书答案
浙教版八年级上册科学书答案
浙教版八年级上册数学书答案
人教版八年级上册语文书答案
沪科版八年级上册数学书答案
北师大版八年级上册数学书答案
人教版八年级上册数学书答案
八年级下册历史课时练答案人教版
人教版八年级下册历史知识与能力训练答案
八年级下册物理伴你学答案苏科版
八年级下册英语课时作业本答案人教版
八年级上册思想品德学法大视野答案人教版
八年级下册历史长江全能学案同步练习册答案人教版
北师大版八年级下册数学书答案
人教版八年级上册英语作业本答案