第3课时第1题答案
D
第3课时第2题答案
6.9
第3课时第3题答案
1125
第3课时第4题答案
（1）设p=kx+b，将点（2，9）与（6，3）代入得
所以售价p（元/千克）
关于上市时间x（月份）的函数关系式为p=-3/2 x+12
（2）设y=a（x-6）2+2，将点（4，3）代入得4a+2=3，解得a=1/4
所以抛物线对应的函数关系式为y=1/4（x-6）2+2=1/4 x2-3x+11，
（3）设收益为M，根据收益=售价-成本，p表示市场售价，y表示成本，
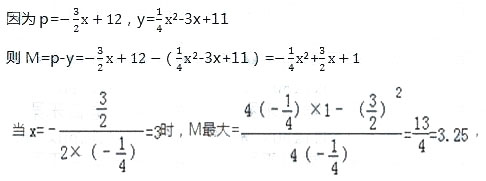
即3月份上市出售这种蔬菜每千克收益最大，最大收益为3.25元
第3课时第5题答案
（1）设抛物线解析式为 y=ax2+bx+c（a≠0）
将A、B、O三点坐标分别代入y=ax2+bx+c 得：
所以所求抛物线为 y=-x2/25
（2）把点（d/2，4-h）代入函数解析式y=-1/25x2，得h=4-1/100d2；
（3）把x=9代入函数解析式y=-1/25x2中，解得：
y=-81/25米，4+2-81/25=69/25=2.76（米）
所以水深超过2.76米时，就会影响过往船只在桥下顺利航行。
第3课时第6题答案
解：（1）y=x（30-3x） 即y=-3x2+30x。
（2）当y=63时，-3x2+30x=63，解此方程得x₁=7，x₂=3
当x=7时，30-3x=9＜10，符合题意
当x=3时，30-3x=21＞10，不符合题意，舍去
∴当AB的长为7 m时，花圃的面积为63 cm2。
第3课时第7题答案
解：（1）y=500-10（x-50）=1000-10x （50≤x≤100）
（2）S=（x-40）（1000-10x）=-10（x-70）2+9000
当50≤x≤70时，利润随着单价的增大而增大。
（3）-10x2+1400x-40000=8000，解得x₁=60，x₂=80
当x=60，成本=16000＞10000，不符合要求，舍去
当x=80，成本=8000＜10000，符合要求
销售单价应定为80元，才能使得一周销售利润达到8000元的同时，投入不超过10000元。
九年级上册物理配套练习册答案人教版
九年级上册数学配套练习册答案青岛版
九年级上册语文配套练习册答案人教版
九年级上册化学配套练习册答案人教版
九年级上册数学配套练习册答案人教版
九年级上册化学课本答案沪教版
华东师大版九年级上册数学书答案
人教版九年级上册化学书答案
人教版九年级上册物理书答案
人教版九年级上册英语书答案
浙教版九年级上册科学书答案
沪科版九年级上册数学书答案
浙教版九年级上册数学书答案
人教版九年级上册语文书答案
北师大版九年级上册数学书答案
九年级下册科学课时特训答案浙教版
九年级下册思想品德作业本答案人教版
九年级上册化学阳光学业评价答案人教版
九年级下册历史与社会思想品德课时特训答案人教版
外研版英语书九年级下册答案
九年级上册语文同步解析与测评答案人教版
九年级下册语文课时作业本答案人教版
九年级下册历史新编基础训练答案人教版
数学九年级上册学习与评价答案苏科版
人教版九年级英语南方新课堂答案