第2课时第1题答案
B
第2课时第2题答案
y=-1/25 x2+6/5 x 0≤x≤30
第2课时第3题答案
16
第2课时第4题答案
解：（1）（130-100）×80=2400（元）；
（2）设应将售价定为x元，则销售利润
当x=125时，y有最大值2500，
所以应将售价定为125元，最大销售利润是2500元。
第2课时第5题答案
解：作DE⊥BC与E
∴∠DEC=∠DEB=90°，
∵∠DAB=∠B=90°，
∴四边形ABED是矩形，
∴∠ADE=90°，AD=BE．AB=DE
∵∠ADC=150°，
∴∠EDC=60°，
∴∠DCE=30°，
∴DC=2DE
设AB=x，则BC=30-x，梯形的面积为S
在Rt△DEC中， 由勾股定理，得
第2课时第6题答案
（1）当X=1时、透光面积最大。
（2）当y=1.5时，x=1，设另一边为 k ，
所以y=kx，带入1.5=k
∴窗框的另一边是1.5 m
解析：y=ax2+bx+c x=0，y=a×02+b×0+c=0，c=0； x=1，
y=a×12+b×1+0=1.5，a+b=1.5； x=2，y=a×22+b×2+0=0，4a+2b=0；
解方程组得a=-1.5，b=3；
y=-1.5x2+3x
观察图像，当x=1 m时，窗户透光面积最大，y最大值=1.5 m2；
当窗户透光面积最大时，窗框的另一边长AD=BC=y/x=1.5/1=1.5（m）。
第2课时第7题答案
（1）设抛物线的解析式为y=ax2+bx+c，由对称轴是y轴得b=0，
因为EO=6，所以c=6，
因为矩形的长BC为8 m，宽AB为2 m，
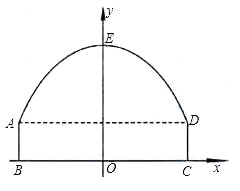
以BC所在的直线为x轴，线段BC的中垂线为y轴，建立平面直角坐标系
所以D（4，2），
又因为抛物线经过点D（4，2），
所以16a+4b+6=2，解得a=−1/4
所求抛物线的解析式为：y=−1/4x2+6
（2）取x=±2.4，代入（1）所求得的解析式中，得
y=−1/4×（±2.4）2+6，
解得：y=4.56＞4.2，
故这辆货运卡车能通过隧道。
第2课时第8题答案
解：（1）以O为原点，顶点为（1，2.25），
设解析式为y=a（x-1）2+2.25过点（0，1.25），解得a=-1，
所以解析式为：y=-（x-1）2+2.25，
令y=0，则-（x-1）2+2.25=0，
解得x=2.5 或x=-0.5（舍去），
所以花坛半径至少为2.5 m
（2）根据题意得出：设y=-x2+bx+c，
把点（0，1.25）（3.5，0）代入
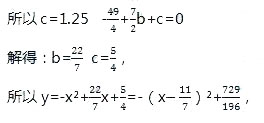
所以水池的半径为3.5 m，
要使水流不落到池外，此时水流最大高度应达729/196米。
九年级上册物理配套练习册答案人教版
九年级上册数学配套练习册答案青岛版
九年级上册语文配套练习册答案人教版
九年级上册化学配套练习册答案人教版
九年级上册数学配套练习册答案人教版
九年级上册化学课本答案沪教版
华东师大版九年级上册数学书答案
人教版九年级上册化学书答案
人教版九年级上册物理书答案
人教版九年级上册英语书答案
浙教版九年级上册科学书答案
沪科版九年级上册数学书答案
浙教版九年级上册数学书答案
人教版九年级上册语文书答案
北师大版九年级上册数学书答案
人教版九年级下册物理配套练习册答案
九年级下册语文长江作业本答案鄂教版
人教版九年级上册历史知识与能力训练答案
北京课改版化学书九年级下册答案
人教版九年级上册英语作业本答案
九年级下册化学书答案上教版
九年级上册数学课课练答案苏科版
浙教版九年级下册数学课本答案
九年级下册语文同步练习答案苏教版
九年级下册英语课时特训答案人教版