第67页复习题C组第1题答案
证明：连接OA、OB、OC，则∠AOB=60°， ∠AOC=36°，
∴∠COB=24°
又360°÷24°=15°，故得证
第67页复习题C组第2题答案
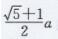
第67页复习题C组第3题答案
证明：如图24-9-55所示，设⊙O的半径为R， AB为⊙O的内接正十边形的一边，连接OA、OB，
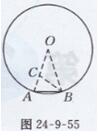
则∠AOB=360°/10=36°，
∠A=∠OBA=1/2 (180°-∠AOB)=72°
以点B为顶点，BA为一边在△OAB的内部作∠ABC=36°，边BC交OA于点C，
则∠OBC=∠OBA-∠ABC=72°-36°=36°，
∠ACB=180°- (∠A+∠ABC)=180°-(72°+36°)=72°
∴∠A=∠ACB，
∴AB=BC
又∵∠AOB=∠OBC=36°，
∴ BC=OC
∴AB=BC=OC
在△OAB和△BAC中，∠A=∠A，∠AOB=∠ABC，
∴△OAB∽△BAC，
∴AB/AC=OA/AB，
第67页复习题C组第4题答案
证明：分点P在⊙O外与点P在⊙O内两种情况：
点P在⊙O外，连接PO分别交⊙O于C、D两点，连接AC、BD(点C在线段PD上，点A在线段PB上)，证明△PAC∽△PDB，
则PA·PB=PC·PD= (OP-R) (OP+R) =OP2-R2；
点P在⊙O内，则有PA·PB=R2-OP2
综上，PA·PB= ∣R2-OP2∣
第67页复习题C组第5题答案
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
北京课改版化学书九年级下册答案
浙教版九年级上册科学课时特训答案
九年级下册历史与社会思想品德课时特训答案人教版
沪教版化学书九年级下册答案
九年级上册化学阳光学业评价答案人教版
九年级下册数学书答案人教版
九年级下册数学新编基础训练答案北师大版
九年级下册化学书答案鲁教版
九年级下册化学课本答案人教版
九年级下册语文作业本答案人教版