习题24.5第1题答案
求证：（1）I与O重合；（2）ID=1/2OB
证明：（1）∵内心为I，∴I为角平分线的交点
∵外心为O，
∴O为各边垂直平分线的交点
又∵等边三角形顶角的平分线、底边上的高重合，
∴I与O重合．故等边三角形的内心、外心重合
（2）∵外接圆半径为OB即IB，内切圆半径为ID，
∴ID⊥BC
∴在Rt△IBD中，∠IBD=30°
∴ID=1/2IB=1/2OB
习题24.5第2题答案
证明：连接IE、IF，
∵AB、AC与OI相切于点F、E，
∴IE⊥AC，IF⊥AB
∴∠AEI+∠AFI=180°
又∵在四边形AEIF中，
∠A+∠EIF+∠AFI+∠AEI=360°，
∴∠A+∠EIF=180°，
∴∠EIF=180°-∠A
∴∠FDE= 1/2∠EIF=1/2(180°-∠A)=90°-1/2∠A
习题24.5第3题答案
解：连接OG、OE、OF
∵OO为△ABC的内切圆，切点为E、F、G，
由题意易知四边形OECF是正方形，
∴FC=EC=r
∴AF=AC-FC=4-r
∵AG=AF，
∴AG=4-r
∵AO平分∠BAC，
∴∠BAD=∠CAD
又∵∠AGO=∠C=90°，
∴△AGO≌△ACD
∴AG/GO=AC/CD，
即4-r/r，
∴r=4/5
习题24.5第4题答案
证明：(1)如图24-5-36所示，△ABC的内切圆⊙I分别与AB、AC、BC切于点D、E、F，连接IE、IF
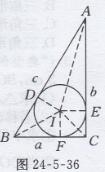
由题意，得四边形IECF是正方形，
∴EC=FC=r,
∴AE= b-r， BF=a-r
∵AE=AD，BF=BD，
∴AD=b-r, BD=a-r
又∵AB=AD+BD=b-r+a-r=c，
∴r=1/2（a+b-c）
(2)连接AI、BI、CI、DI
∵S△ABC=S△ABI+S△BCI+S△ACI=1/2c
R+1/2a•r+1/2b•r=1/2r（a+b+c），
又∵S△ABC=1/2ab，
∴1/2ab=1/2r(a+b+c)，
∴r=ab/a+b+c
习题24.5第5题答案
证明：由点E为内心， 得∠BAD=∠CAD
∴DB=DC，∴DB=DC
连接EC，则BCD=∠BAD=∠CAD， ∠BCE=∠ACE，
而∠DCE=∠DCB+∠BCE， ∠DEC=∠CAD+∠ACE，
∴∠DCE= ∠DEC，
∴DC=DE
∴DB=DC=DE
习题24.5第6题答案
解：4个，三条直线围成一个三角形，它的三个内角平分线的交点为三角形的内心，它到三边的距离相等，三角形的外角平分线所在的三条直线两两相交，得三个交点，称为这个三角形的旁心，它们分别到三条已知直线的距离也是相等的，故符合条件的点共4个。
习题24.5第7题答案
解：如图24-5-37所示，AB、BC、AC分别切⊙O于点F、D、E点，
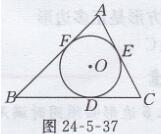
∴AF=AE，BF=BD, CD=CE
设AF=AE=x cm，BF=BD=y cm，CD=CE=z cm，
故AF=4 cm，BD=9 cm，CE=5 cm
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
译林牛津版九年级下册英语课本答案
九年级下册历史新编基础训练答案华师大版
九年级上册语文同步训练答案人教版
九年级下册物理同步练习答案苏科版
九年级上册英语学法大视野答案人教版
九年级上册思想品德课时练答案人教版
九年级下册历史新编基础训练答案北师大版
九年级下册语文伴你学答案苏教版