习题24.4第1题答案
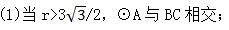
习题24.4第2题答案
已知：如图24-4-46所示，
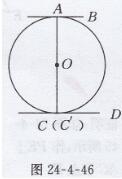
AB切⊙O于点C, CD切⊙O于点C， 且AB//CD，
求证：AC是⊙O的直径。
证明：连接AO并延长交CD于Cˊ点
∵AB切⊙O于点A，
∴OA⊥AB
∵AB∥CD，
∴OAICD，垂足为C，
又∵CD切⊙O于点C，
∴OA⊥CD的垂足为C
∴点Cˊ与点C重合
∴AC是⊙O的直径。
习题24.4第3题答案
解：如果圆的两条切线互相平行，则连接两个切点的线段是圆的直径。
习题24.4第4题答案
证明：连接OD，则OA=OD，
∴∠ODA=∠A
又∵OC//AD
∴∠COB=∠A，∠ODA=∠COD，
∴∠COD=∠COB
又∵OC=OC，OB=OD，
∴△OBC≌△ODC
∴∠ODC=∠OBC= 90°，
即OD⊥DC
∴DC是⊙O的切线
习题24.4第5题答案
证明：连接OD
∵CD=BD，AO=BO，
∴OD//AC
∵DE⊥AC,
∴DE⊥OD
∴DE是⊙O的切线
习题24.4第6题答案
证明：由点D作DF_LAC于点F
∵AD是∠BAC的平分线，
∴DF=DB
（1）AC⊥DF且点F为半径外端，故AC为OD的切线。
（2）∵Rt△EBD≌Rt△CFD，
∴EB=CF
由切线长定理可得AB=AF，
∴AC=AF+FC=AB+EB
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
九年级下册英语课时作业本答案人教版
苏科版九年级上册数学书答案
九年级上册语文课课练答案苏教版
人教版九年级上册物理作业本答案江西省
九年级上册物理课课练答案苏科版
人教版九年级下册数学南方新课堂答案
九年级下册数学伴你学答案苏科版
九年级下册数学新编基础训练答案通用s版
九年级下册物理同步练习答案苏科版