复习题B组第104页第1题答案
解：3个。因为多边形的外角和为360°，则外角中的钝角最多有3个，所以相邻的内角中，最多有3个锐角。
复习题B组第104页第2题答案
证明：如图19-5-27所示，
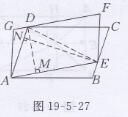
连接DE，过D作DM⊥AE于M，
过E作EN⊥AD于N
∵S△ADE=1/2AD·EN=1/2S□ABCD
S△ADE=1/2AE· DM=1/2S□AEFG ，
∴S□ABCD= S□AEFG
复习题B组第104页第3题答案
证明：如图19-5-28所示，
过点E作EG//AB交AN于点G，连接DG，EN
∵四边形ABCD为平行四边形，
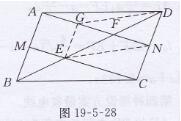
∵AB//=CD
∴EG// CD
∵M，N分别是AB，CD的中点，
∴AM//=CN，
∴ 四边形AMCN为平行四边形，
∴AN// CM
∴EG=CN（夹在两条平行线间的平行线段相等），
即EG//=DN
∴ 四边形EGDN是平行四边形
∴EF=FD
同理可证EF=BE
∴ BE=EF=FD
复习题B组第104页第4题答案
证明：如图19-5-29，作OE⊥AB于点E，
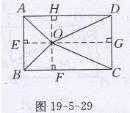
OF⊥BC于点F，OG⊥CD于点G，OH⊥AD于点H
在 Rt△OAE中，OA2=AE2+OE2
Rt△OBE中，OB2=BE2+OE2
Rt△ODG中，OD2=OG2+DG2
Rt△OCG中，OC2=CG2十OG2
由作图可知四边形AEOH，OHDG，EOFB，OFCG为矩形，
∴ AE=DG，BE=GC，
∴ OA2+OC2=OB2+OD2
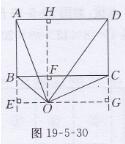
如果点O在矩形ABCD的外部，结论还成立。
如图19-5-30所示，同理可证
复习题B组第104页第5题答案
证明：如图19-5-31所示，连接PE，PD
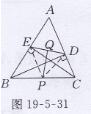
∵BD⊥AC，CE⊥AB，P是BC的中点，
在Rt△BCE和Rt△BCD中，
PE=1/2BC，PD=1/2BC，
∴PE=PD
又∵Q是DE的中点，
∴ PQ⊥DE（等腰三角形三线合一）
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
人教版八年级下册数学作业本答案江西省
八年级上册物理课堂精练答案北师大版
八年级下册物理书答案苏科版
八年级下册英语同步训练答案人教版
物理八年级下册学习与评价答案苏科版
苏科版八年级上册生物伴你学答案
沪粤版八年级上册物理作业本答案江西省
浙教版八年级上册科学课时特训答案
八年级下册地理阳光学业评价答案人教版
八年级下册物理课课练答案苏科版