习题19.3第7题答案
解：如图19-3-17所示，
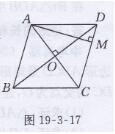
在菱形ABCD中，AC=6 cm，BD=8 cm，
且AC⊥BD于点O
∴AO=3 cm，BO=4 cm
在Rt△ABO中，
∵S菱形ABCD=1/2AC·BD=CD·AM，
∴1/2×6×AM，
∴AM=4.8 cm
即平行线AB与CD之间的距离为4.8 cm
习题19.3第8题答案
解：连接AC，BD，则AC=BD
∵E，N分别是AB，AD的中点，
∴EN=1/2BD
同理MF=1/2BD，
∴EN=MF=1/2BD
同理可证EM=NF=1/2AC
∴EM=MF=NF=NE
∴四边形EMFN为菱形
习题19.3第9题答案
证明：如图19-3-39所示
∵四边形ABCD是平行四边形，
∴AD//BC，
∴∠DAC= ∠BCA.
又∵∠BAC= ∠DAC，
∴∠BAC=∠ BCA，
∴□ABCD是菱形
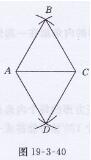
习题19.3第10题答案
作法：（1）作线段AC=3 cm
（2）分别以A，C为圆心，以3 cm为半径画弧，两弧相交于点B，D
（3）连接AB，BC，AD，CD，则四边形ABCD就是所求作的菱形
示意图如图19-3-40所示
习题19.3第11题答案
证明：∵AB//CD，AD//BC，
∴ 四边形ABCD为平行四边形，
如图19-3-41所示，
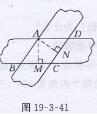
过点A作AM⊥BC于点M，AN⊥CD于点N
∵纸条等宽，
∴AM=AN
∵S□ABCD =BC· AM=CD· AN，
∴BC= CD
∴□ABCD为菱形
习题19.3第12题答案
证明：∵DE⊥AC， DF⊥AB，
∴∠DFA=∠DEA=90°
又∵∠A=90°，
∴四边形AEDF为矩形，
∵D是BC的中点，
∴DB=DC
又∵BF=CE，
∴Rt△BFD≌Rt△CED，
∴F=DE，
∴四边形AEDF为正方形
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
八年级下册英语长江全能学案阅读训练答案人教版
八年级上册数学学法大视野答案湘教版
北师大版八年级下册数学作业本答案江西省
八年级下册历史同步导学与优化训练答案人教版
八年级上册地理学法大视野答案湘教版
八年级下册数学南方新课堂答案人教版
八年级下册英语配套练习册答案人教版
八年级下册数学同步精练答案北师大版
八年级下册英语课时练答案人教版
八年级上册英语配套练习册答案人教版