习题19.2第11题答案
证明：∵AB⊥l，CD⊥l，
∴ AB//CD
又∵AB=CD，
∴四边形ABDC是平行四边形
∴AC//BD，即AC//l
习题19.2第12题答案
已知：如图19-2-47所示，在□ABCD中，
E，F分别是AB，CD的中点，且AC与EF交于点O
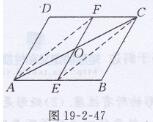
求证：OE=OF，OA= OC
证明：连接AF，CE
∵E，F分别是口ABCD的边AB，CD
的中点，
∴AE= 1/2AB，CF= 1/2CD，
∴ AE= CF
又∵CF//AE，
∴ 四边形AECF是平行四边形．
∴AC，EF互相平分，即OE=OF，CH=CC
习题19.2第13题答案
已知：如图19-2-48所示，
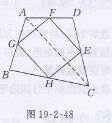
在四边形 ABCD中，H，E，F，G分别为各边的中点，
求证：四边形HEFG为平行四迦形
证明：连接AC
∵F，E分别是AD，DC的中点，
∴EF//AC， EF=1/2AC（三角形中位线定理）
同理GH//AC，GH=1/2AC，
∴GH//=EF
∴ 四边形HEFG为平行四边形
习题19.2第14题答案
证明：如图19-2-49所示，连接EF
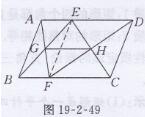
在□ABCD中，AD//=BC，
∵AE=BF，
∴DE=CF
∴AE//=BF，
∴ 四边形ABFE是平行四边形
∴ BG= EG，同理EH=CH
∴GH//BC，GH=1/2BC
习题19.2第15题答案
证明：如图19-2-25所示，
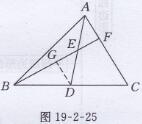
去BF的中点G，链接DG，
∵D，G分别是BC，BF的中点，
∴DG//AG=1/2CF，
∴∠DAC=∠ADG，∠AFE=∠EGD
又∵AE=DE，
∴△AEF≌△DEG
∴DG=AF，∴AF=1/2FC
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
八年级下册语文伴你学答案苏教版
八年级下册历史与社会作业本答案人教版
八年级上册英语同步解析与测评答案人教版
生物八年级上册学习与评价答案苏教版
八年级上册语文同步训练答案人教版
八年级下册历史长江全能学案同步练习册答案人教版
八年级下册生物课课练答案苏科版
人教版八年级上册数学课时练答案
八年级上册数学学法大视野答案湘教版
人教版八年级下册物理作业本答案江西省