复习题B组第65页第1题答案
证明：（1）设∠A为x度，
由题意知x+2x+3x=180，解得x=30，
所以∠A=30°，∠B=60°，∠C=90°
所以△ABC是直角三角形且c=2a
由勾股定理，得c2 =a2+b2，
即（2a）2=a2 +bx，b2=3a2
（2）设∠A为x度，由题意知x+-x+ 2x=180，解得x=45
所以∠A=∠B=45°，∠C=90°
所以△ABC是直角三角形且a=6
由勾股定理得c2=a2+b2，所以c2=-2a2
复习题B组第65页第2题答案
解：由折叠的性质，知AQ=AB=10 cm，PQ=PB
在Rt△ADQ中，
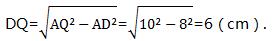
∴CQ=CD-DQ=10-6=4（cm）
设CP=x，则PB=PQ=8-x
在Rt△PCQ中，由勾股定理，得，PQ2=CP2+CQ2，
即（8-x）2=x2+42，解这个方程得x=3
∴PQ=8-x=5（cm）
复习题B组第65页第3题答案
解：设两直角边分别为a、b，斜边为c
（1）以a，b，c为边的等边三角形的高分 别为h₁，h₂，h₃
即S₁+S₂=S₃
（2）S₁=1/2π（a/2）2=π/8a2，
S₂=1/2π·（b/2）2=π/8b2，
S₃=1/2π（c/2）2=π/8c2
由勾股定理，得a2 +b2=c2，
所以S₁+S₂=π/8a2+π/8b2=π/8（a2+b2）=π/8c2，
即S₁+S₂=S₃
（3）发现结论：以直角三角形的三边为边向形外作相同边数的正多边形或以三边为直径作半圆，所得图形的面积之间始终存在这样的关系： S₁+S₂=S₃
复习题B组第65页第4题答案
证明：∵在△ABC中，∠C= 90°，
∴a2 +b2 =c2
∵（ka）2+（kb）2=k2 （a2 +b2）=k2c2=（kc）2，
k为正整数，a，b，c为勾股数，
∴ka，kb，kc也是勾股数
复习题B组第65页第5题答案
证明：∵（m2-n2）2+（2mn）2
=m⁴ -2m2n2+n⁴+4m2n2
=m⁴+2m2n2+n⁴
=（m2 +n2）2，
∴m2+n2，2mn，m2-n2是勾股数
复习题B组第65页第6题答案
解：∵△APC绕点A逆时针旋转得到△AP'B，
∴AP'=AP=6，P' B=PC=10，
∠P'AB=∠PAC
又∵∠BAP+∠PAC= ∠BAC=60°，
∴∠P'AB+∠BAP=∠P'AP=60°，
∴△AP'P为等边三角形，
∴∠P'PA=60°，PP'=6
又∵P'B=10，PB=8，PP'=6，
∴pp'2+PB2 =P'B2，
∴△P'PB为直角三角形，∠P'PB=90°
∴∠APB=∠APP'+∠P'PB=150°
复习题B组第65页第7题答案
（1）
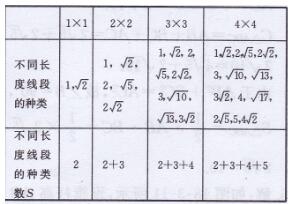
（2）S=n2+3n/2（n≤4，n为整数）
（3）不成立
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
语文八年级下册学习与评价答案苏教版
人教版八年级上册英语长江作业本答案
物理八年级下册学习与评价答案苏科版
八年级下册生物长江全能学案同步练习册答案人教版
八年级上册英语同步解析与测评答案人教版
浙教版八年级上册科学作业本答案
八年级上册思想品德同步解析与测评答案人教版
人教版八年级上册英语作业本答案
教科版八年级上册物理作业本答案江西省
八年级下册物理课课练答案苏科版