习题17.4第1题答案
解:设长方形的长和宽分别是a和b,
由一元二次方程根与系数的关系得 a+b=-12/4=3,ab=3/4
∴长方形的周长为2(a+b) =2×3=6,
面积为ab=3/4
习题17.4第2题答案
解:原方程可化为3x2-5x-7=0,
∵a=(-5) 2-4×3×(-7)=109>0,
∴原方程必有两个不相等的实数根
设方程的两根为x1,x2,
由一元二次方程根与系数的关系可得
x1+x2=-5/3=5/3,x1•x2=-7/3
∴方程的两根之和为5/3,两根之积为-7/3
习题17.4第3题答案
解法1:设方程的另一个根为x1,
∵方程的一个根是1/2,
∴1/2x1=-3/2,∴x1=-3
∵x1+x2=-m/2,∴m=5
∴方程的另一根为-3,m的值为5
解法2::1/2是方程2x2+mx-3=0的一个根,
∴2×(1/2)2+m×1/2-3=0,解得m=5
∴原方程可化为2x2+5x-3=0,根据求根公式,
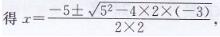
解得x1=1/2,x2=-3
即方程的另一个根是-3,m的值是5
习题17.4第4题答案
解:∵方程的根的判别式为0,
∴方程有两个相等的实数根,
则方程的另一根也为2
∵2+2=-m,∴m=-4
又∵2×2=2m-n,即4=-8-n,
∴n=-12
习题17.4第5题答案
解:因为两数的和为2,积为-2,以这两数为根的方程为x2-2x-2=0

 苏科版八年级下册数学书答案
苏科版八年级下册数学书答案 北师大版八年级下册数学书答案
北师大版八年级下册数学书答案 八年级下册物理书答案北师大版
八年级下册物理书答案北师大版 译林牛津版八年级下册英语课本答案
译林牛津版八年级下册英语课本答案 苏教版八年级下册语文课本答案
苏教版八年级下册语文课本答案 人教版八年级下册英语课本答案
人教版八年级下册英语课本答案 北师大版八年级下册生物课本答案
北师大版八年级下册生物课本答案 北师大版八年级下册历史课本答案
北师大版八年级下册历史课本答案 浙教版八年级下册科学课本答案
浙教版八年级下册科学课本答案 人教版八年级下册生物课本答案
人教版八年级下册生物课本答案 人教版八年级下册生物知识与能力训练答案
人教版八年级下册生物知识与能力训练答案 人教版八年级上册物理知识与能力训练答案
人教版八年级上册物理知识与能力训练答案 青岛版八年级上册数学书答案
青岛版八年级上册数学书答案 八年级下册语文作业本答案人教版
八年级下册语文作业本答案人教版 八年级下册物理新编基础训练答案人教版
八年级下册物理新编基础训练答案人教版 八年级上册数学配套练习册答案人教版
八年级上册数学配套练习册答案人教版 八年级上册数学学法大视野答案华东师大版
八年级上册数学学法大视野答案华东师大版 浙教版八年级上册科学课时特训答案
浙教版八年级上册科学课时特训答案 八年级下册历史同步精练答案人教版
八年级下册历史同步精练答案人教版