第198页习题第1题答案
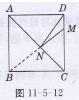
解:如图11-5-12所示,链接BN交AC于点N,
∵点B,D关于直线AC对称,
∴BN=DN,此时DN+MN的值最小。
在Rt△BCM中,
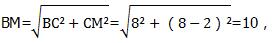
∴DN+MN的最小值是10
第198页习题第2题答案
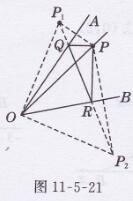
解:如图11-5-21所示,分别作点P关于直线OA的对称点P₁,
关于直线OB的对称点P₂,连接P₁P₂,
交OA于点Q,交OB于点R,
此时△PQR的周长最小.连接OP₁,OP₂.
∵∠AOB-45°,∴∠P₁OP₂ =90°,
∵OP₁=OP=OP₂=10,
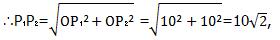
即△PQR周长的最小值是10
第198页习题第3题答案
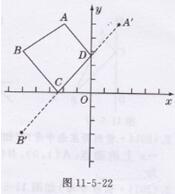
解:如图11-5-22所示,分别作点A关于y轴的对称点A′(2,5),点B关于x轴的对称点B′(-5,-3)
连接A′B′交x轴于点C,交y轴子点D,此时的C,D使四边形ABCD周长最小
第198页习题第4题答案
解:(1)把A(2,0),B(0,4)代入y=kx+b
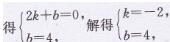
所以一次函数的表达式是y=2x+4
(2)如图11-5-23所示,找出点C关于y轴的对称点C′,连接DC′交y轴于点P,连接DC,此时PC+PD的值最小,
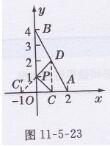
∵A(2,0),C为OA的中点,∴C(1,0),
∴C′(-1,0),∴CC′=2
∵A(2,0),B(0,4),D为AB的中点,
∴D(1,2),
∴CD=2 ,CD⊥x轴,
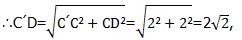
即PC+ PD的最小值为2,此时点P(0,1)
第198页习题第5题答案
解:∵点D关于直线AC的对称点是点B,
∴当P为BE与AC的交点时,PD+PE的值最小
∵△ABE是等边三角形,
∴BE=AB=2,
∴PD+PE的最小值为2
第198页习题第6题答案
习题1~5题都用到了轴对称;
“挑战自我”中用到了旋转;
“交流与发现”问题(5)、(6)用到了平移;
“观察与思考”问题 (1)用到了轴对称,问题(2)、(3)用到了平移和轴对称。
受到的启发:
平面图形中的最短路径问题:不管在什么背景下,有关线段之和最短问题,一般都是化归到“两点之间的所有连线中,线段最短”,而转化的方洼大都是借助于 “轴对称点”,而其中的求值问题一般都是利用勾股定理解答。

 苏科版八年级下册数学书答案
苏科版八年级下册数学书答案 北师大版八年级下册数学书答案
北师大版八年级下册数学书答案 八年级下册物理书答案北师大版
八年级下册物理书答案北师大版 译林牛津版八年级下册英语课本答案
译林牛津版八年级下册英语课本答案 苏教版八年级下册语文课本答案
苏教版八年级下册语文课本答案 人教版八年级下册英语课本答案
人教版八年级下册英语课本答案 北师大版八年级下册生物课本答案
北师大版八年级下册生物课本答案 北师大版八年级下册历史课本答案
北师大版八年级下册历史课本答案 浙教版八年级下册科学课本答案
浙教版八年级下册科学课本答案 人教版八年级下册生物课本答案
人教版八年级下册生物课本答案 八年级下册历史新编基础训练答案北师大版
八年级下册历史新编基础训练答案北师大版 语文八年级上册学习与评价答案苏教版
语文八年级上册学习与评价答案苏教版 八年级下册思想品德新课程自主学习与测评答案人教版
八年级下册思想品德新课程自主学习与测评答案人教版 八年级下册物理课课练答案苏科版
八年级下册物理课课练答案苏科版 八年级上册语文同步解析与测评答案人教版
八年级上册语文同步解析与测评答案人教版 八年级下册思想品德同步精练答案粤教版
八年级下册思想品德同步精练答案粤教版 语文八年级下册学习与评价答案苏教版
语文八年级下册学习与评价答案苏教版 八年级上册物理配套练习册答案沪科版
八年级上册物理配套练习册答案沪科版 人教版八年级上册语文作业本答案江西省
人教版八年级上册语文作业本答案江西省 八年级上册数学配套练习册答案人教版
八年级上册数学配套练习册答案人教版