习题11.2第6题答案
解：EM= EN
证明：如图11-2-32所示，
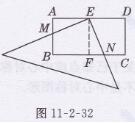
在矩形ABCD中，AD=2AB，E是AD的中点，
过点E作EF⊥BC于点F，则有AB=AE=EF=FC,
∵∠AEM∠DEN=90°，∠FEN+∠DEN= 90°，
∴∠AEM=∠FEN
在Rt△AME和Rt△FNE中，
∠AEM=∠FEN,AE=FE，∠MAE=∠NFE，
∴Rt△AME≌Rt△FNE，
∴EM=EN
习题11.2第7题答案
解：如图11-2-33所示，
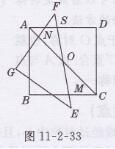
设EF与AD的交点为S，
则与BM保持相等的线段有DS，GN
证明 :∵ ∠AOS =∠COM，∠SAO=∠MCO=45°，AO=CO，
∴△AOS≌ △COM( ASA)
又∵ AD=BC，
∴AD-AS=BC-CM，即 DS=BM
∵∠F= ∠OCM= 45°
FO= CD，∠FON=∠COM
∴△FON≌COM(ASA) ,
∴FN= CM.
又∵GF=BC,
∴GF- FN= BC-CM
即GN=BM
习题11.2第8题答案
解：如图11-2-34所示，
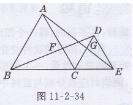
设AC与BD相交于点F， AE与CD相交于点G，
△ACE，△ACG，△ECG绕点C逆时针旋转60°可分别得到△BCD，△BCF，△DCF
习题11.2第9题答案
解：他的想法正确。
证明：如图11-2-35所示，
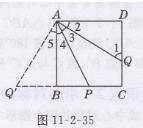
把△ADQ绕点A按顺时针方向旋转90°， 得到△ABQ′，
则∠2=25，∠1=∠Q′，
且Q′，B，P三点在同一条直线上
根据题意，得∠1=∠BAQ，
∴∠1=∠3+∠4
∵∠2=∠3，
∴∠5=∠3，
∴∠1=∠5+∠4=∠Q′AP，
∴∠Q′ =∠Q′AP，
∴PA=Q′P
∵Q′P=PB+Q′B ，Q′B=DQ
∴Q′P =PB+DQ，
∴PA=PB+DQ
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
八年级上册历史学法大视野答案人教版
八年级下册物理同步训练答案人教版
河北少儿版八年级下册生物作业本答案江西省
八年级下册英语阳光学业评价答案沪教版
八年级下册数学书答案沪科版
八年级下册地理新编基础训练答案湘教版
人教版八年级上册思想品德新课程自主学习与测评答案
数学八年级上册轻轻松松学数学冀教版
八年级下册语文书答案人教版
八年级下册语文阳光学业评价答案人教版