习题11.2第1题答案
解：△BDF可以看作是由△ADC按逆时针方向旋转90°得到的，旋转中心是点D旋转是90°
习题11.2第2题答案
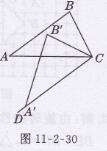
解：如图11-2-30所示，△A′B′C为△ABC旋转后的图形。
习题11.2第3题答案
解：∵∠PBP′=∠ABC= 90°，P′B=PB=3，在Rt△PBP′中， 由勾股定理，
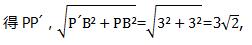
∴PP′的长是3
习题11.2第4题答案
解：(1) S△D′A′B=1/2S矩形ABCD = 1/2ab；
S△DBC =1/2S矩形ABCD =1/2ab；
S△D′BD =1/2BD′ ×BD=1/2c2
(2) S梯形A′CDD′=1/2(A′D′+ CD)×(A′B+BC)=1/2（a十b）2，
S梯形A′CDD′=S△D′A′B+S△DBC+SAD′BD=1/2ab+1/2ab+=1/2c2=ab+1/2c2
(3)能，
∵S△D′A′B+S△DBC+S△D′BD
=S梯形A′CDD′，
∴1/2ab+1/2ab+1/2c2=1/2(a+b)2，
∴2ab+c2=(a+b)2，
∴2ab+c2=a2+2ab+b2，
∴c2=a2+b2
习题11.2第5题答案
解：（1）如图11-2-31所示，
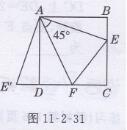
△ADE′为旋转后得到的图形．
（2）∵△ADE′是E′由△ABE绕点A按顺时针方向旋转90°得到的，
∴BE=DE′，∠BAE=∠DAE ,E′，D，F三点在同一条直线上，
∴∠E′AD+ ∠DAF=∠BAE+∠DAF=90°-45°=45°.
在△AE′F与△AEF中，AF=AF，AE′=AE,∠E′AF=∠EAF,
∴AAE′F≌△AEF,
∴EF= E′F=E′D+ DF=BE+DF=2+3=5(cm)
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
八年级上册历史学法大视野答案人教版
八年级下册物理同步训练答案人教版
河北少儿版八年级下册生物作业本答案江西省
八年级下册英语阳光学业评价答案沪教版
八年级下册数学书答案沪科版
八年级下册地理新编基础训练答案湘教版
人教版八年级上册思想品德新课程自主学习与测评答案
数学八年级上册轻轻松松学数学冀教版
八年级下册语文书答案人教版
八年级下册语文阳光学业评价答案人教版