习题11.1第6题答案
解：∵点C(-1，3)与F(4，O)是一组对应点，
∴4-（-1）=5，0-3= -3
∴点F可以看作由点C向右平移5个单位长度，再向下平移3个单位长度得到的
∵A(-3，5)，B(-2，1)，
∴D(-3+5，5-3)，E(-2+5，1-3)
即D(2，2)，E(3，-2)
习题11.1第7题答案
B′(-5，1)，C'(-4，-5)，D′(-1，- 6)
习题11.1第8题答案
解：“柳叶”形的面积=1/4·π·42+12×4-1/4·π·42=4，
所以“柳叶”形的面积是4，
弧DG沿DE方向平移一个单位长度得到弧EB
习题11.1第9题答案
解：（1）AC⊥CE.理由如下：
∵BD//CE，且BD⊥AC，∴AC⊥CE
（2）相等，理由如下：
因为这两个三角形等底、等高
（3）∵S△ACD=S△BEC，
∴S梯形ABCD=S△AEC
又∵ AC2CE，
∴S△AEC=1/2AC · CE
=1/2AC·BD=1/2ab，
∴S梯形ABCD=S△AEC=1/2ab
习题11.1第10题答案
解：∵CD和EF的长为定值，
∴四边形CDEF的周长最小时，ED与CF之和最小
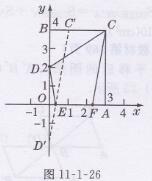
如图11-1-26所示，过点E作EC′//FC，与BC交于点C′，
由平移的性质，FC=EC
在y轴上作与点D关于x轴对称的点D′，
则ED= ED′，显然，要使ED与CF之和最小，
只需使ED′与EC′之和最小，当C′，E，D′三点在同一条直线上时，
ED′与EC′之和最小，
∵C(1，4)，D′(0，- 2)
设直线CD′的表达式为y=kx+b(k≠0)，
∴直线CD′的表达式为y =6x-2
∵点E在直线C′D′上，且纵坐标为0，
∴x=1/3
∴点E的坐标为（1/3，0），
点F的坐标为（7/3，0）
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
八年级下册数学作业本答案浙教版
八年级上册数学配套练习册答案青岛版
人教版八年级上册历史知识与能力训练答案
八年级上册数学同步解析与测评答案人教版
沪粤版八年级上册物理作业本答案江西省
人教版八年级上册思想品德新课程自主学习与测评答案
北师大版八年级下册数学作业本答案江西省
八年级下册生物同步解析与测评答案人教版
八年级上册英语同步解析与测评答案人教版
八年级上册历史阳光学业评价答案人教版