第159页综合练习第6题答案
解：（1）甲、乙两根蜡烛燃烧前的高度分别是30 cm，25 cm
（2）设甲蜡烛燃烧时y与x之间的函数表达式为y=k₁x+b₁（k₁≠0），
由图可知，函数的图象过点（2，0），（0，30）
∴y= -15x+30
设乙蜡烛燃烧时y与x之间的函数表达
式为y=k₂x+b₂ （kx≠0）
由图可知，函数的图象过点（2、5，0），（0，25），
∴y= -10x+25
（3）由题意，得-15x+30=-10x+25，解得x=1，
所以，当燃烧t h的时候，甲、乙两根蜡烛剩余部分的高度相等
观察图象可知：当0≤x<1时，甲蜡烛的剩余高度比乙蜡烛的剩余高度高；
当1<x<2.5时，甲蜡烛的剩余高度比乙蜡烛的剩余高度低
第159页综合练习第7题答案
解：由5x-y=9，得y= 5x-9
由2y+x=4，得y=-x/2+2
在同一直角坐标系中分别画出直线l₁：y=5x-9与直线
l₂：y=-2+2的图象，如图10-7-7所示
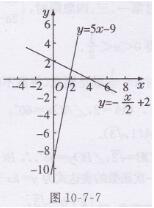
由图可以看出，直线l₁与l₂相交于点（2，1），
所以原方程组的解是
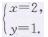
第159页综合练习第8题答案
解不等式-2x+1>0，得x<1/2
第159页综合练习第9题答案
解：因为乙学生原来在甲学生的前方，但两人在A处相遇，
说明此时甲学生追上乙学生，所以甲学生快，
64/8-64-16/8=8-6=2（m/s），
甲学生的速度比乙学生的速度每秒快2（m/s）
第159页综合练习第10题答案
解：（1）当一次函数y=ax+2a-1的图象
经过第一、二、三象限时，
此时a=1满足题意（答案不唯一）
（2）当一次函数y=ax+2a-1的图象
经过第二、三、四象限时，
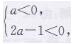
解得a<0.此时a=-1满足题意（答案不唯一）
（3）当一次函数y=ax+2a-1的图象
经过第一、三、四象限时，
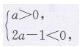
解得0<a<1/2
此时a=1/3满足题意（答案不唯一）
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
八年级下册语文课课练答案苏教版
八年级下册地理新编基础训练答案湘教版
八年级上册英语学法大视野答案人教版
八年级下册生物长江作业本答案人教版
八年级下册数学长江全能学案同步练习册答案人教版
八年级下册英语同步解析与测评答案人教版
青岛版八年级上册数学书答案
人教版八年级上册思想品德新课程自主学习与测评答案
八年级下册地理新课程自主学习与测评答案人教版
八年级下册语文作业本答案人教版