习题10.6第1题答案
解：（1）由左到右依次填14，17，20
（2）把梯形个数n作为自变量，用横轴表示，所拼得的四边形周长1看作n的函数，用纵轴表示，建立直角坐标系，把表中每一对（n，1）的值作为点的坐标，在直角坐标系中描出表中相应的点，发现这些点在同一条直线上（如图10-6-4所示）
这个函数是一次函数，表达式为L=3n+2（n为正整数）
（3）当n=20时，L=62
习题10.6第2题答案
解：（1）图象如图10-6-5所示
猜想：y是x的一次函数
设函数表达式为y=kx+b（k≠0），根据题意，
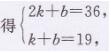
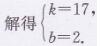
所以函数表达式为y= 17x+2（x为正整数）
（2）对角线的长度
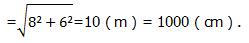
由题意，得17x+2≥1 000×2，
解得x≥117又9/17
答：至少要制作118个纸杯。
习题10.6第3题答案
解：（1）y=150×6x+260×5（20-x）=-400x+26000
所以y与x之间的函数表达式为y=-400x+26 000
（2）由题意，得-400x+26 000≥24 000，
解得x≤5，20-5=15
所以至少要安排15名工人制造乙种零件。
习题10.6第4题答案
解：按方案（1）购买所需费用
y₁=200×20+（x-20）×40=40x+3 200；
按方案（2）购买所需费用
y₂=200×20×90%+40xX90%=36x+3600
当y₁=y₂时，
40x+3200=36x+3600
解得x=100
当y₁>y₂时，
40x+3200>36x+3600，
解得x>100
当y₁<y₂时，
40x+3 200<36x+3600
解得x<100
所以当x=100时，两种购买方案费用相同；
当x>100时，选择方案（2）省钱；
当20<x<100时，选择方案（1）省钱
习题10.6第5题答案
解：（1）由题意知，汽车在15 min内行驶
的路程是20-10=10（km）
汽车的平均速度为10÷15/60=40（km/h）
y与x之间的函数表达式为y=40x+10
（2）不能
理由如下：当y=150+30=180时，
10+40x=180，
∴x=17/4
∵8+17/4>12，
∴汽车按原速不能到达
当y=150时，10+40x=150，
∴x=3.5，30÷（12 -8 -3.5）=30×2=60（km/h），
∴要在12:00前赶到C站，那么汽车车速最少应提高到60 km/h
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
苏教版八年级上册语文伴你学答案
人教版八年级上册语文作业本答案江西省
八年级下册英语同步解析与测评答案人教版
八年级下册语文阳光学业评价答案人教版
人教版八年级下册生物作业本答案江西省
八年级上册数学学法大视野答案华东师大版
人教版八年级上册思想品德新课程自主学习与测评答案
人教版八年级上册思想品德作业本答案
人教版八年级上册语文课时特训答案