第108页综合练习第13题答案
解：∵不等式3x-k<0的解集为x≤k/3，
又∵不等式的正整数解为1，2，3，
∴3≤k/3<4
∴9≤k<12
又∵是取整数值，
∴k=9，10，11
第108页综合练习第14题答案
解：解不等式组x-b>0，
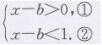
解不等式①，得x>b
解不等式②，得x<b+1
∴不等式组的解集为6<x<6+1
又∵任何一个x的值均不在2≤x≤5的范围内，
∴b+1≤2或b≥5
∴b≤1或b≥5
第108页综合练习第15题答案
解：p满足的不等关系是③④
第108页综合练习第16题答案
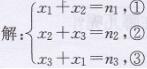
①-②，得x₁-x₃=n₁-n₂
∵n₁>n₂，
∴x₁-x₃>0，
∴x₁>x₃
②-③，得x₂- x₁=n₂-n₃
∵n₂>n₃，
∴x₂-x₁>0，
∴x₂>x₁
∴x₃<-x₁<x₂
第108页综合练习第17题答案
解：（1）设购进乙种电冰箱x台，
则购进甲种电冰箱2x台，
丙种电冰箱（80 -3x）台，根据题意，得
1200×2x+1600x+2000（80-3x）≤132000
解不等式，得x≥14
答：至少购进乙种冰箱14台。
（2）当甲种电冰箱台数不超过丙种电冰箱台数时，
2x≤80-3x，
∴x≤16
又∵x≥14且x取整数，
∴x=14，15 ，16，
∴有三种方案：
方案一：甲种电冰箱28台，
乙种电冰箱14台，
丙种电冰箱38台．
方案二：甲种电冰箱30台，
乙种电冰箱15台，
丙种电冰箱35台，
方案三：甲种电冰箱32台，
乙种电冰箱16台，
丙种电冰箱32台，
①当x=14时，总费用为1200×2×14+1 600×14+2 000 （80 -3×14）=132000（元）
②当x=15时，总费用为1200×2×15+1 600×15+2 000 （80 -3×15）=130000（元）
③当x=16时，总费用为1200×2×16+1 600×16+2000 （80 -3×16）=128000（元）
答：当购买甲、乙、丙三种电冰箱分别为32台，16台，32台时，最省钱。
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
八年级上册物理学法大视野答案人教版
八年级下册科学课时特训答案浙教版
八年级下册语文配套练习册答案人教版
八年级下册思想品德长江作业本答案人教版
八年级下册物理新编基础训练答案人教版
苏教版八年级上册思想品德补充习题答案
八年级上册语文同步解析与测评答案人教版
人教版八年级下册语文作业本答案江西省