习题7.4第6题答案
解：△FEC为直角三角形，
理由：设正方形的边长为4x，
∵E为AB的中点，
∴AE=EB=2x.
又∵AF=1/4AD，
∴AF=x，FD=3x
在△AEF中，EF2=AF2+AF2=(2x) 2+x2=5x2
同理，CE2=20x2，CFv=25xv，
∴EF2+CE2=CF2，
∴△FEC为直角三角形
习题7.4第7题答案
(1)解：当m=3，n=2时，
m2=n2=5，2mn=12，
m2+n2=13
∵52+122=132，
∴(5，12，13)是一个勾股数组
(2)证明：∵m>n，m，n都是正整数，
∴m2-n2，2mn，m2+n2都是正整数，且m2+n2的值最大，
∵（m2-n2）2=m4 -2m2n2+n4，
(2mn) 2=4m2n2，
(m2+n2)2=m4 +2m2n2 +n4，
∴(m2-n2)2+(2mn) 2=(m2+n2)2
∴当m>n，m，n都是正整数时，(m2-n2，2mn，m2+n2)是一个勾股数组
习题7.4第8题答案
解：（1）第1个数为奇数；
（2）两个连续整数且偶数在前，奇数在后；
（3）第1个数的乎方等于后两个数的和；
（4）第4组勾股数为(9，40，41)；
（5）(2n+l，2n2+2n，2n2+2n+1)，（m，m2-1/2，m2+1/2）
习题7.4第9题答案
证明：如图7-4-9所示。
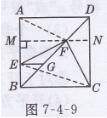
连接AF，过点F作EM⊥AB，垂足为M，交于点N，连接EC
∵四边形ABCD为正方形，
∴AB⊥AD
又∵EG//AD，
∴EG⊥AB
∵F为DG的中点，
∴M为AE的中点，
设正方形的边长为1，DN=x，
则FN=AM=DN=x,
∴NC=MF=1-x，BE=1-2x
在 Rt△MEF中 ,
FE2=x2+(1-x) 2=2x2-2x+l
同理 , FC2= 2x2-2x+l, .
EC2=(1- 2x) 2+12=4x2-4x+2
∴FE2+FC2=EC2，
∴△EFC为直角三角形，
即EF⊥FC
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
八年级下册地理新课程自主学习与测评答案人教版
数学八年级上册轻轻松松学数学冀教版
八年级下册思想品德新课程自主学习与测评答案人教版
八年级上册物理学法大视野答案人教版
八年级上册地理阳光学业评价答案人教版
人教版八年级下册生物作业本答案江西省
八年级下册思想品德长江作业本答案人教版
八年级下册历史课时练答案人教版
人教版八年级下册物理南方新课堂答案