习题7.2第6题答案
解：只要测量出BC与CD的长就可求出旗杆的高度。
设BC=a，CD=b，旗杆的高为h，
则在Rt△ABD中，AB=h，BD=a+b，AD=h+a，
可得h2+(a+b) 2=(h+a)2，
则h=2ab+b2/2a
习题7.2第7题答案
解：如图7-2-10所示，连接BD交EF于点O，连接BE
由折叠知：EF⊥BD且O为BD的中点，
∴EB=ED
又∵四边形ABCD为矩形，
∴∠A=90°，
在Rt△ABE中，设BE=x，则AE=8-x，
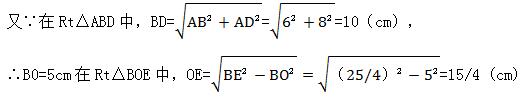
∴x2-(8-x)2=62，
∴x=25/4，
由三角形全等知EO= OF，
∴EF=2EO=15/2 cm
即折痕EF的长为15/2 cm
习题7.2第8题答案
解：设左边较大正方形的边长为x cm，右边较大正方形的边长为y cm，
则x2+y2 =49
设正方形A，B，C，D的边长分别为a cm，b cm，c cm，d cm，
则有a2+b2=x2，c2+d2=y2，
∴SA+SB+SC+SD=a2+b2+c2+d2=x2+y2=49 (cm2)
∴正方形A，B，C，D面积的和为49(cm2)
习题7.2第9题答案
解：如图7-2-17所示，
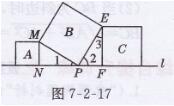
由题意知：在Rt△MNP和Rt△PFE中，
∠MNP=∠PFE，MP=PE
又∵∠1+∠2=90°，∠2+∠3=90°，
∴∠1=∠3，
∴△MNP≌△PFE(AAS)，
∴MN= PF，NP= FE
又∵MN2+NP2=MP2，MN2 =5，EF2=11，
∴MP2=5+11=16，
即正方形B的面积为16
习题7.2第10题答案
（1）证明：∵四边形ABCD是矩形，
∴AB=DC，∠B=∠C=90°
在Rt△ABP中，AB2=PA2-PB2
在Rt△PDC中，DC2=PD2-PC2
∴PA2-PB2=PD2-PC2，
即PA2+PC2=PB2+PD2
（2）解：（1）中的等式成立。
证明：如图7-2-18所示，
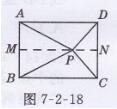
过点P作MNIAB，垂足为M，交于点N
∵四边形ABCD是矩形，
∴AB//DC，∴MN⊥DC
在RtAPAM中，PA2=AM2+MP2
在RtAPBM中，PB2=BM2+MP2
在RtAPDN中，PD2=PN2+DN2
在Rt△PNC中，PC2=PN2+NC2
∴PB2-PA2=BM2-AM2
PC2-PD2=CN2-DN2
由题意，得AM-DN，BM=CN
∴PB2-PA2=PC2-PD2
即PA2+PC2=PB2+PD2
（3）解：（1）中的等式成立。
证明：如图7-2-19所示，
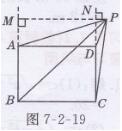
过P作PM⊥AB，交BA的延长线于点M，交CD的延长线于点N，则PN⊥CD
在Rt△PAM中，PA2=PM2+AM2，
在Rt△PBM中，PB2=PM2+BM2，
在Rt△PDN中，PD2=PN2+DN2，
在Rt△PCN中，PC2=PN2+CN2，
∴PB2-PA2=BM2-AM2,
PC2-PD2=CN2-DN2
∵ AM=DN , BM= CN ,
∴ PB2-PA2=PC2- PD2 ,
即PA2+PC2=PB2+PD2
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
人教版八年级上册生物作业本答案江西省
八年级下册英语课时练答案人教版
浙教版八年级上册数学书答案
八年级下册历史长江全能学案同步练习册答案人教版
八年级上册语文同步练习答案苏教版
物理八年级下册学习与评价答案苏科版
八年级下册地理南方新课堂答案人教版
八年级下册生物课时练答案人教版
八年级上册数学配套练习册答案青岛版
八年级下册生物同步精练答案北师大版