综合练习第58页第8题答案
解：（1）能求也当x=3时y的值，根据表格中的信息，根据抛物线的轴对称性可知，
x=3时的函数值与x=-1时的函数值相等
∴当x=3时，y=-4
（2）设这个二次函数的表达式是y=a(x-1) 2-2
∵当x=-1时，y=-4，
∴-4=a(-1-1) 2-2，解得a=-1/2，
∴y=-1/2(x-1) 2-2， 即y=-1/2x2+x-5/2，
∴该二次函数的表达式是y=-1/2x2+x-5/2
综合练习第58页第9题答案
∴这个二次函数的表达式是y=x2+2x-5
∵x=-b/2a=-2/2×1=-1
∴y=x2+2x-5的图象的对称轴是直线x=-1
(2)答案不唯一。如y=1x2+x-5，y=-x2-2x-5
综合练习第58页第10题答案
解：（1）画出抛物线y-x2-5x+2（如图5-8-12所示）
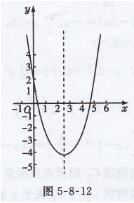
观察图象，找出图象与x轴的公共点，可以发现图象与x轴的公共点的横坐标在0与1之间以及4与5之间
借助计算器可以估计一元二次方程x2-5x+2-0的近似解为x1≈0.4或0.5，x2≈4.5或4.6
（2）画出抛物线y=x2+x-7（如图5—8-13所示）
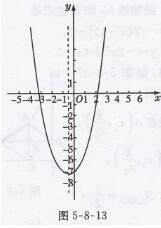
观察图象，找出图象与x轴的公共点，可以发现图象与x轴的公共点的横坐标在-4与-3之间以及2与3之间
借助计算器可以估计一元二次方程x2+x-7=0的近似解为x1≈-3.1或-3.2，x2≈2.1或2.2
综合练习第58页第11题答案
解：∵顶点在x轴上，
∴(-2b) 2-4×1×4=0，解得b=±2
综合练习第58页第12题答案
解：∵a>0，
∴抛物线y=ax2+bx+c开口向上
∵b>0，
∴-2b<0，
∴抛物线y= ax2+bx+c的对称轴在y轴左侧
∵c<0，
∴抛物线y=ax2+bx+c与x轴的交点在y轴的负半轴上
∵a-b+c=0，
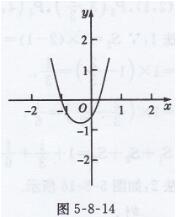
∴抛物线y=ax2+bx+c与x轴交于点(-1，0)
图象草图如图5-8-14所示
综合练习第58页第13题答案
解：（1）这天0时到6时，该水池的蓄水量y(m3)与时间x(h)之间的函数表达式是
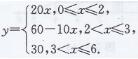
（2）y与x之间的函数图象如图5-8-15所示
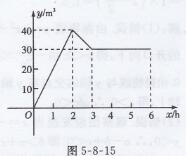
点拨：当2<x≤3时，
y=40+[10(x-2)-20(x-2)]
=40+(10x-20-20x+40)
=40+10x-20-20x-l-40
=-10x+60
综合练习第58页第14题答案
C
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
九年级下册数学同步解析与测评答案人教版
九年级思想品德新编基础训练答案人教版
苏科版九年级上册数学伴你学答案
人教版九年级上册数学新课程自主学习与测评答案
九年级下册数学新编基础训练答案北师大版
九年级下册物理书答案苏科版
苏科版九年级上册物理补充习题答案
人教版九年级上册语文书答案