习题5.6第1题答案
解：（1）∵b2-4ac=12-4×（-1/4）× (-1) =1-1=0，
∴二次函数y=-1/4x2+x-1的图象 与x轴有公共点，有一个公共点
（2）∵b2-4ac=l-4×1×2=1-8=-7< 0
∴二次函数y=x2+x+2的图象与x轴无公共点
（3）∵b2—4ac=(-3) 2-4×l×（-4)=9+16=25>0
∴二次函数y=x2-3x-4的图象与x轴有公共点，有两个公共点
习题5.6第2题答案
解：画出二次函数y=-1/2x2-2x+l的图象，如图5-6-12所示
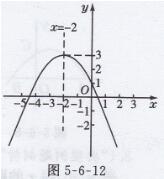
观察图象，找出图象与x轴的公共点，可以发现图象与x轴的公共点的横坐标在-5与-4之间以及0与1之间
借助计算器，可以估计一元二次方程-1/2x2-2x+l=0的近似解为xl≈-4.5或-4.4
习题5.6第3题答案
解：∵抛物线y=x2+3x+m与x轴有两个交点，
∴一元二次方程x2+3x+m=0中，b2-4ac>0,
∴32-4×1×m>0,
∴m<9/4
∴当m<9/4时，抛物线y=x2+3x+m与x轴有两个交点。
习题5.6第4题答案
解：（1）x1=1，x2=3
（2）1<x<3，1<x<3
（3）y=-2x2+8x-6
习题5.6第5题答案
解：观察图象可得抛物线y=ax2—3x+a2 -1经过点(0，0)，
把点(0，0)的坐标代入y=ax2-3x+a2-1，得a2-1=0，解得n=±1
∵抛物线开口向下，
∴a<0，
∴a=±1
习题5.6第6题答案
解：二次函数y=ax2+2x-5的图象一定经过点（0，-5），对称轴为直线x=-2/2a=-1/a
当抛物线y=ax2+2x-5与x轴有交点时，
4-4a×（-5）≥0，
解得a≥-1/5
（1）当a>0时，如图5-6 -13所示，
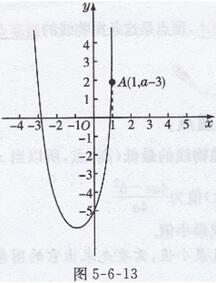
∵当x=1时，y-a×12+2×1-5=a-3，
∴点A的坐标为(1，a-3)
又当x=0时，y=-5，
结合图象知a-3>-5，解得a>-2
当a-3>0，即a>3时，抛物线y=ax2+2x-5与x轴一定有一个交点的横坐标大于0而小于1
∴当a>3时，一元二次方程ax2+2x-5=0的两根中有—个根大于0而小于1
（2）-1/5≤a<0时，a-3<0，如图5-6-14所示，点（1，a-3）一定在x轴下方，
抛物线y=ax2+2x-5与x轴交点的横坐标一定大于1，与已知相矛盾。
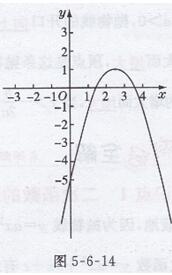
综上，当a>3时，关于x的一元二次方程ax2+2x-5=0的两根中有一个根大于0而小于1
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
九年级下册物理同步练习答案苏科版
九年级下册数学伴你学答案苏科版
北师大版九年级上册数学书答案
九年级下册语文新编基础训练答案人教版
九年级下册思想品德课课练答案苏人版
人教版九年级上册数学长江作业本答案
九年级下册语文作业本答案人教版
九年级下册物理书答案苏科版
人教版九年级下册语文南方新课堂答案
九年级上册化学配套练习册答案人教版