习题5.5第1题答案
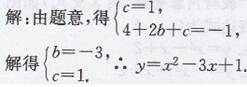
∵当x=-l时，y=(-1)2-3×（-1）+1=1+3+l=5，
∴点P(-1，2)不在这个二次函数的图象上。
习题5.5第2题答案
解：∵AB=1.6 m，
∴点A到y轴的距离为1/2AB=0.8 m
∵涵洞顶部到底面的最大高度是2.4 m，
∴点A到x轴的距离为2.4 m
又∵点A在第三象限，
∴点A的坐标为(-0.8，-2.4)
设抛物线所对应的二次函数表达式为y=ax2，
∴-2.4=a•(-0.8)2，
∴a=-15/4，
∴抛物线所对应的二次函数表达式为y=-15/4x2
习题5.5第3题答案
解：由二次函数y=ax2+bx+c的图象得，它的图象经过（-1，0），(0，3)，(3，0)三点，
方法1：根据题意，得
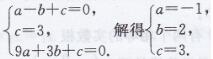
∴这个函数的表达式是y=x2+2x+3
方法2：设这个函数表达式是y=a(x+1)（x-3），
把点(0，3)代人上式，得3=a(0+1)（0-3），
∴a=-1
∴这个函数的表达式是y=-(x+1)(x-3)，
即y=-x2+2x+3
习题5.5第4题答案
解：将点(0，-1)与(3，5)的坐标代入y=ax2+bx+c中，
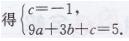
又∵对称轴是直线x=1，
∴-b/2a=1
∴这个二次函数的表达式是y= 2x2-4x-1
习题5.5第5题答案
解：（1）设过B，E，F三点的二次函数的表达式为y=ax2+bx+c
∵正方形ABCD的边长为4，
∴EO=1/2×4=2，
∴点E的坐标为(0，2)
同理点F的坐标为(2，0)，点B的坐标为(-9，- 2)
∴二次函数的表达式为y=-3/4x2+1/2x+2
（2）
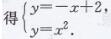
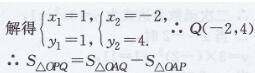
习题5.5第6题答案
解：（1）∵抛物线y=ax2+bx+c经过点(0，1)，(2，-3)，
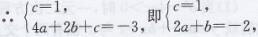
∴只要符合c=1，2a+b=-2即可
如：y=-x2+1，y=x2-4x+l等
（2）若抛物线开口向下，则a<0
若对称轴在了轴的左侧，则-b/2b <0，
∴b<0
又∵6= -2-2a，
∴-2-2a<0，
解得a>-1，故a的取值范围是- 1<a<0
鲁教版语文书九年级下册答案
北师大版数学书九年级下册答案
人教版语文书九年级下册答案五四制
华东师大版数学书九年级下册答案
苏科版数学书九年级下册答案
湘教版数学书九年级下册答案
鲁教版数学书九年级下册答案五四制
译林版英语书九年级下册答案
沪教版英语书九年级下册答案
外研版英语书九年级下册答案
九年级下册数学新编基础训练答案通用s版
九年级上册英语学法大视野答案人教版
九年级上册物理学法大视野答案人教版
九年级下册语文作业本答案人教版
人教版九年级下册数学作业本答案江西省
九年级下册语文课课练答案苏教版
北京课改版化学书九年级下册答案
人教版九年级下册物理作业本答案江西省
沪科版九年级上册数学书答案
九年级下册物理新编基础训练答案通用y版