练习第101页第1题答案
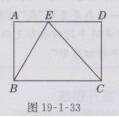
解：如图19-1-33所示，四边形ABCD是矩形，
所以AD//BC，AB⊥BC，所以AD与BC间的距离处处相等且都等于AB，
所以△BCE的边BC上的高的长等于AB的长，
S矩形ABCD=AB•BC，
S△BCE=1/2AB•BC
故△BCE的面积等于矩形ABCD面积的一半。
练习第101页第2题答案
解：如图19-1-16所示，
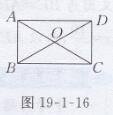
解：因为四边形ABCD为矩形，所以AC=BD，所以AO=BO=1/2AC=1/2BD
因为∠AOB=60°，
所以△AOB为等边三角形，
所以AO=AB=3.6，
所以AB=BD=7.2，
在Rt△ABD中，由勾股定理得AB2+AD2=BD2，
即3.62+AD2=7.22，
即AD2=38.88，所以AD≈6.2
练习第101页第3题答案
解法1：（面积法）如图19-1-21，过点P作PE⊥AC于点E，PE⊥BD于点F,
∵AB=8，BC=15，
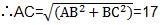
∴1/12×8/2×15=1/2×17/2×PE+1/2×17/2×PE，
∴PE+PF=120/17
解法2：如图19-1-21，过点P作PE⊥AC于点E，PE⊥BD于点F，AG⊥BD于点G，PM⊥AG于点M
∵因为四边形ABCD为矩形，
∴OA=OD，
∴∠1=∠2
∵AB=8，BC=15，
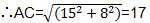
∴BD=17
根据△ABD的面积的1/2AD•AB=1/2BD•AG，
∴AG=(15×8)/17=120/7
∵AG⊥BD，PF⊥BD，PM⊥AG，
∴四边形PMGF是矩形（有三个角市直角的四边形四边形是矩形），
∴PE=MG
又∵∠DAG+∠1=90°,
∠APE+∠2=90 °，
∴∠DAG=∠APE.
在Rt△APM和Rt△PAE中，∠AMP=∠PEA=90°，∠DAG=∠APE，AP=PA，
∴△APM ≌ △PAE(AAS),
∴PE=AM，
∴PF+PE=MG+AM=AG=120/17
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
八年级下册物理课时作业本答案人教版
八年级下册物理长江全能学案同步练习册答案人教版
人教版八年级上册英语书答案
教科版八年级下册物理作业本答案江西省
八年级下册历史新编基础训练答案北师大版
华东师大版八年级上册数学书答案
八年级下册英语作业本答案人教版
八年级下册数学书答案人教版
八年级下册英语阳光学业评价答案沪教版
苏教版八年级上册语文伴你学答案