华东师大版数学书八年级下册第94页复习题答案(3)

第94页复习题第13题答案

证明：如图18-3-32所示。  

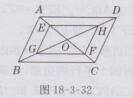
∵四边形ABCD是平行四边形， 

∴OA=OC，OB=OD， 

又∵AE=CF，BG=DH， 

∴OA-AE=OC-CF，

OB-BG=OD-DH，

即OE=OP，OG=OH

∴四边形EGFH是平行四边形（对角互相平分的四边形是平行四边形）

∴GH=HE（平行四边形的对边相等）

第94页复习题第14题答案

证明：如图18-3-33，   

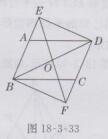
∵四边形ABCD是平行四边形， 

∴AB//CD,OB=OD, 

∴∠ABD=∠BDC，

∵∠BOE=∠DOF，

∴△BOE ≌ △DOF，

∴OE=OF 

∴四边形BEDE是平行四边形 

（对角互相平分的四边形是平行四边形）

第94页复习题第15题答案

证明：如图18-3-34所示，

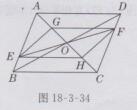
∵四边形ABCD是平行四边形， 

∴AB//CD，OB=OD，OA=OC， 

∴ ∠ABD=∠BDC, 

又∵∠BOE=∠DOF， 

∴△BOE ≌ △DOF, 

∴OE=OF， 

∵OA=OC，G，H分别为OA,OC的中点，

∴OG=OH 

∴四边形EHFG是平行四边形 

（对角互相平分的四边形是平行四边形）

第94页复习题第16题答案

解：作平行四边形方法很多，如：

（1）画两组对边分别平行的四边形得到平行四边形（见教材72页试一试）

（2）画两组对边分别相等的四边形得到平行四边形（见教材82页试一试）

（3）画一组对边平行且相等的四边形得到平行四边形（见教材83页试一试）

（4）画一个两条对角线互相平分的四边形得到平行四边形（见教材85页试一试）

（5）已知：如图18-3-35所示，线段a，b及∠a。

       

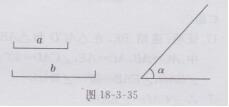
求作:□ABCD，使AB=a，BC=b，∠B=∠a，

作法：①作∠MBN=∠a；

②在BM上截取BA=a，在BN上截取BC=b；

③分别以A，C为圆心，一BC，BA长为半径作弧，使两弧交于点D；

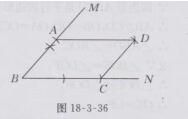
④连接AD，CD，则四边形ABCD就是求作的平行四边形，如图18-3-36所示，

          

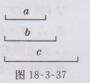
（6）已知如图18-3-37所示， 已知线段a，b，c

 

求证：□ABCD，使AB=a，AC=b，BC=c，

作法：①作线段BC=c；

②分别以BC为圆心，以a,b长为半径作弧，使两弧交于点A；

③连接AB，AC；

④再分别以A,C为圆心，以c，a长为半径作弧，使两弧交于点D；

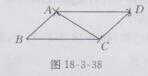
⑤连结AD，CD，则四边形ABCD就是所求作的平行四边形，如图18-3-38所示。

第94页复习题第17题答案

证明：连结BE，在△ACD和△ABE中，AC=AB，AD=AE，∠CAD=60°-∠BAD，∠EAB=60°-∠BAD，

∴∠CAD=∠EAB， 

∴△ACD ≌ △ABE，

∴CD=BE，∠ABE=∠ACD=60° 

∵CD=BF，

∴BE=BF， 

∴△BEF是等边三角形， EF=BE=BF，

∴EF=DC, 

又∵∠ABC=∠EFB=60° 

∴EF//BC，即EF//DC, 

∴四边形CDEF是平行四边形

第94页复习题第18题答案

解：有四个平行四边形，分别是 □ABCD，□AFCE，□BFDE和□EGFH。 

证明如下：在 □ABCD中，有AD//BC， 

∴∠EAO=∠FCO，

又在△EAO和△FCO中，有AO=CO,∠AOE=∠COF， 

∴△EAO ≌ △FCO，

∴EO=FO， 

∴四边形AFCE是平行四边形， 

∴AE//=FC，

∴ED//=DF， 

∴四边形BFDE是平行四边形， 

∵AF//EC，BE//DF， 

∴四边形EGFH是平行四边形，故连同已知的平行四边形共有四个平行四边形。

第94页复习题第19题答案

解：如图18-3-39所示，应添加DG=AE。

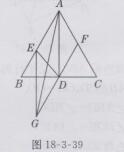
∵FD//AB，

∴DG//AE，

又∵DG=AE，

∴四边形AEGD是平行四边形

（一组对边平行且相等的四边形是平行四边形）

∴AG与ED互相平分（本题答案不唯一）