习题18.2第1题答案
解：当两个全等三角形是锐角三角形时，可以拼成6个四边形；当两个全等三角形是直角三角形或钝角三角形时，可以拼成4个四边形，但是两个全等三角形拼成的4个四边形，但是两个全等三角形拼成的四边形中，只有3个是平行四边形，因为对边分别相等的四边形是平行四边形。
习题18.2第2题答案
证明：如图18-2-36所示，
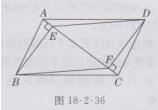
∵四边形ABCD是平行四边形，
∴AB=CD，AB//CD，
∴∠BAC=∠ACD，
∵BE⊥AC，DF⊥AC
∴BE//DF，∠AEB=∠CFD=90°，
∴△ABE ≌ △CDF，
∴BE=DF，
∴四边形BEDF是平行四边形
（一组对边平行且相等的四边形是平行四边形）
习题18.2第3题答案
证明：如图18-2-37所示。
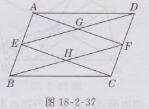
∵四边形ABCD是平行四边形，
∴AB=//CD，AB=CD，
∵E,F分别是AB，CD的中点，
∴AE=BE=CF=DF，
∴AE∥=CF，BF∥=DF，
∴四边形BFDF与四边形AECF都是平行四边形。
∴BF∥DE，AF∥CE，即EG∥FH，EH∥FG，
∴四边形EHFG是平行四边形
（两组对边分别平行的四边形是平行四边形）
习题18.2第4题答案
证明：如图18-2-38所示
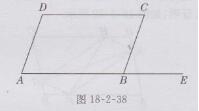
∵∠C=∠CBE，
∴AB∥DC,
∵AB=DC，
∴四边形ABCD是平行四边形
（一组对边平行且相等的四边形是平行四边形）
∴AD=BC
习题18.2第5题答案
证明：如图18-2-39所示，连接DM。
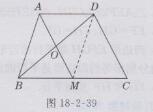
∵AM，BD互相平分，
∴四边形ABMD是平行四边形，
∴AD∥BM，AD=BM，
∵M是BC的中点，
∴BM=CM，
∴AD=CM，
又∵AD∥CM,
∴四边形AMCD是平行四边形
（一组对边平行且相等的四边形是平行四边形）
∴AM∥=DC
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
八年级下册地理新编基础训练答案湘教版
八年级下册数学课时特训答案浙教版
外研版八年级上册英语课时特训答案
八年级下册语文书答案人教版
人教版八年级上册语文新课程自主学习与测评答案
八年级上册物理书答案人教版
苏教版八年级上册生物伴你学答案
浙教版八年级上册科学作业本答案
沪科版八年级上册数学书答案