青岛版数学书九年级下册习题5.1答案

习题5.1第1题答案

解：（1）方法1：观察表格发现如果向容器内注水1 s，水面高度增加2 cm 

∴如果向容器内注水t s，水面高度增加2t cm

由于容器内原有水面的高度是50 cm 

∴h与t之间的函数表达式是h=2t+50，t≥0  

方法2：假设h与t之间的函数表达式是h=kt+6，

把t=5，h=60；t=10，h=70 代入函数表达式，

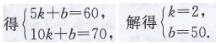
∴h与t之间的函数关系可能是h=2t+50

把表中t与h的数值代入h=2t+50中验证

可得表中所有t与h的对应值都满足h=2t+50，

所以h与t之间的函数表达式是h=2t+50，t≥0

（2）把t=18代入h=2t+50中，得h=2×18+50=86(cm)

所以当t=18 s时，水面高度是86 cm。

习题5.1第2题答案

解：由图象可知y与x之间的关系是一次函数关系，设其表达式为y=kx+6

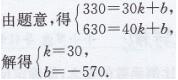
所以表达式为y=30x-570 

当y=0时，0-30x-570，解得x=19

所以免费托运质量的范围是0≤x≤19

习题5.1第3题答案

解：（1）v=2t；

（2）0≤t≤20；

（3）当t=3.5 s时，v=2×3.5=7(m/s)； 

（4）由16=2t，得t=8，所以当t=8s时，小球的速度为16 m/s

习题5.1第4题答案

解：（1）由函数图象知y与x之间的函数是分段函数，并且每段函数都是一次函数

当10≤x≤40时，设y与x之间的函数表达式是y=k₁x+b₁(10，2000)，(30，3000)代入该式，

 

所以这段函数的表达式是y=50x+1500，10≤x≤40

当x=40时，y=50x+1500=50×40+1500=3500（kg）

由于在40天后每天的需水量比前一天增加100妇，

所以当x=41时，y=3500+100=3600(kg)

当x>40时，设y与x之间的函数表达式为y=k²x+b²，

将x=40，y=3500； x=41，y=3600代人该式，得 

所以这段函数的表达式是y=100x-500,x>40。 

由此得到y与x之间的函数表达式是 

   

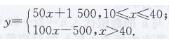
（2）根据题意，得

100x-500≥4000，

100x≥4 500，

x≥45

所以应从第45天开始进行人工灌溉

习题5.1第5题答案

解：（1）温度，长度

（2）观察表格得到当温度为10℃时，合金棒的长度是10.01 cm。 

（3）10.05，10.15 

（4）观察表格得到合金棒在x=0℃时的长度y=10 cm，

温度每升高5℃，合金棒的长度增加0.005 cm

则温度每升高1℃，合金棒的长度增加0.001 cm，

所以当温度为x℃时，合金棒的长度为(10+0.001x) cm

所以y与x之间的函数表达式是y=0.001x+10

（5）当x=-20℃时，y=0.001×(-20)+10=9.98(cm). 当x=100℃时，y=O. 001×100+10=10.1(cm) 

答：当温度是-20℃时，合金棒的长度是9.98 cm；当温度是100℃时，合金棒的长度是10.1 cm

习题5.1第6题答案

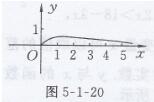
解：在这个问题中，输出数y与输入数x之间的函数关系是用列表法表示的，用函数表达式表示为y=x/x²+1，用图象法表示如图5-1-20所示

习题5.1第7题答案

（1）由四边形APCD的面积y=正方形ABCD的面积-△ABP的面积

习题5.1第8题答案

解：（1）最先到达终点的是乙队，它比甲队提前的时间是：5-4.4=0.6(min).即乙队比甲队提前0.6 min到达终点。 

（2）点A坐标为(1，100)，它表示的实际意义是乙队1 min前进了100 m

点B坐标为(3，450)，它表示的实际意义是甲、乙两队3 min都前进了450 m，即甲、乙两队经过3 min相遇。

（3）乙队在第一次加速后的速度为450-100/3-1=175(m/min)， (800-100)÷175=4(min)

所以乙队在第一次加速后，继续保持这个速度前进，再需用4 min才能到达终点。

即乙队从起点开始共需用5 min才能到达终点。