能力提升第1题答案
（1）x₁=1，x₂=-3
（2）先化为一般形式，再选择合适的解法，x₁=2，x₂ =-8
能力提升第2题答案
k=1
由题意得k2+3k-4=0，解得k1=1，k2=-4
当k=1时，原方程化为5x₂+3x=0，
解得x₁=0,x₂=-3/5，符合题意；
当k=-4时，原方程不是一元二次方程，故k=1
能力提升第3题答案
周长为15
解x2-9x+18=0
得x₁=3， x₂=6，
以3，3，6为边不能构成三角形
以3，6，6为边可以构成三角形，其周长为15
能力提升第4题答案
设x2+x=m，则m2 -2m-3 =0，
解得 m₁=3，m₂=-1
当m=3时，x₂+x=3，即x2+x-3=0，
A=13>0，故x2+x-3=0有实数解；
当m=-1时，x2+x=-1，即x2+x+1=0，△=-3<0，
x2+x+1=0无实数解，不合题意，舍去
所以x2 +x=3
能力提升第5题答案
（1）△=（-6）2-4·1·（-k2）=36+4k2>0，
故无论k为任何实数，该方程都有两个不相等的实数根；
（2）根据根与系数的关系，x₁x₂=-k2，x1+x2=6，
又x₁+2x₂=14，故x₁=-2，x₂=8
因为k2=-x₁x₂ =16，所以k=±4
能力提升第6题答案
△=[-（2k+3)]2-4(k2 +3k+2)=1>0，
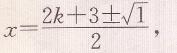
即x₁=（2k+3+1）/2=k+2，x₂=（2k+3-1）/2=k+1
（1）若BC=5为斜边，则(k+1)2+（k+2）2=52，
解得k₁=-5（舍去），k₂=2
若k+2为斜边，则(k+1)2+52=（k+2）2，
解得k=11
综上，k=2或11时，△ABC是直角三角形；
（2）若k+2=5，则k=3，此时k+1=4，三边长分别为4，5，5，周长为14
若k+1=5，则k=4，此时k+2=6，三边长分别为5，6，5，周长为16
综上，当k=3或4时，△ABC是等腰三角形，等腰三角形ABC的周长为14或16
九年级上册物理同步解析与测评答案人教版
九年级上册英语同步解析与测评答案人教版
九年级上册数学同步解析与测评答案人教版
九年级上册语文同步解析与测评答案人教版
九年级上册历史同步解析与测评答案人教版
九年级上册化学课本答案沪教版
华东师大版九年级上册数学书答案
人教版九年级上册化学书答案
人教版九年级上册物理书答案
人教版九年级上册英语书答案
浙教版九年级上册科学书答案
沪科版九年级上册数学书答案
浙教版九年级上册数学书答案
人教版九年级上册语文书答案
北师大版九年级上册数学书答案
苏人版九年级上册思想品德伴你学答案
九年级下册英语新编基础训练答案译林版
沪教版英语书九年级下册答案
语文九年级上册学习与评价答案苏教版
九年级下册数学书答案青岛版
九年级下册数学同步训练答案人教版
九年级上册历史学法大视野答案人教版
九年级上册化学配套练习册答案人教版
北师大版数学书九年级下册答案