同步学习第（一）题答案
1、C
2、BC=EF(或BE=CF)
3、连接BD，利用“边边边”证△ABD≌△CBD
同步学习第（二）题答案
1、A
2、90
3、平行。利用“边角边”证△AED≌△CEF， 则∠A =∠FCE，所以AB//CF
同步学习第（三）题答案
1、D
2、△DOC，“AAS”
3、利用“角边角”证△ABE≌△ACD， 可得AD =AE，则AB -AD =AC-AE，即BD=CE
同步学习第（四）题答案
1、A
2、CB
3、∠ABC+∠DFE=90o
理由如下：在Rt△ABC和Rt△DEF中，
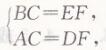
∴Rt△ABC≌Rt△DEF (HL)
∴∠ABC =∠DEF
又∠DEF+∠DFE=90°
∴∠ABC+∠DFE=90°
同步学习第（五）题答案
1、B
2、平行
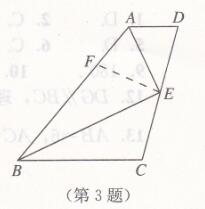
3、如图，在AB上截取AF=AD
∵ AE平分∠DAB，
∴∠DAE=∠FAE,
∵BE平分∠ABC，
∴ ∠FBE=∠CBE
在△DAE和△FAE中 ,
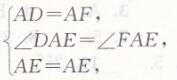
∴△DAE≌△FAE
∴∠D =∠AFE
∵AD //BC ,
∴∠D+∠C=180°
∵∠AFE+∠BFE = 180°
∴∠BFE=∠C
在△FBE和△CBE中 ,
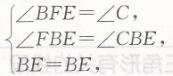
∴△FBE≌△CBE (AAS)
∴BF=BC
∴ AB=AF+BF=AD+BC
同步学习第（六）题答案
1、C
2、1 cm<AD<6 cm
3、已知：如图，在△ABC和△A'B'C'中， AB =A'B'，AC=A'C'，AM和A 'M'是中线，且 AM=A 'M’
求证：△ABC≌△A'B’C’
证明：分别延长AM和A'M'到D和D'，使得 MD=AM，M'D' =A'M'，连接CD和C'D '
在△AMB和△DMC中，
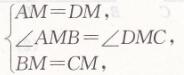
∴△AMB≌△DMC (SAS)
∴AB =DC，∠3= ∠D
同理，A’B’=D，C’，∠4=∠D’
∵AB=A’B', ∴ CD=C’D’
又AD =2AM=2A'M' =A 'D',AC =A 'C',
∴△ACD≌△A 'C'D'(SSS)
∴∠1=∠2，∠D=∠D'
∴∠3=∠4，∠BAC=∠B'A'C'
∴△ABC≌△A'B'C' (SAS)
八年级上册物理同步解析与测评答案人教版
八年级上册语文同步解析与测评答案人教版
八年级上册历史同步解析与测评答案人教版
八年级上册思想品德同步解析与测评答案人教版
八年级上册英语同步解析与测评答案人教版
八年级上册物理书答案人教版
华东师大版八年级上册数学书答案
青岛版八年级上册数学书答案
人教版八年级上册英语书答案
浙教版八年级上册科学书答案
浙教版八年级上册数学书答案
人教版八年级上册语文书答案
沪科版八年级上册数学书答案
北师大版八年级上册数学书答案
人教版八年级上册数学书答案
八年级下册历史长江作业本答案川教版
八年级上册语文学法大视野答案语文版
苏教版八年级下册语文课本答案
八年级下册地理新编基础训练答案湘教版
人教版八年级上册生物知识与能力训练答案
语文八年级上册学习与评价答案苏教版
人教版八年级上册语文课时特训答案
八年级下册语文同步训练答案人教版
生物八年级上册学习与评价答案苏教版