习题5.4第7题答案
81/2 cm2
解析：如图5-5-31所示
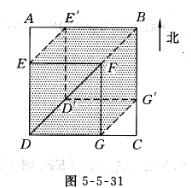
（1）根据题意可知BF =3 cm，
所以正方形ABCD的对角线长为DF+ FB=9 cm，
所以正方形ABCD的面积为1/2×9× 9= 81/2（cm2)
习题5.4第8题答案
95°
解析：此题属拐角、折线问题，通常通过作平行线来解决问题，
如图5-5-32所示，
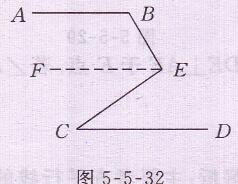
过点E作EF∥AB， 则AB∥EF∥CD
因为∠ABE=120°，∠DCE= 35°，
所以 ∠BEF =60°，∠FEC=35°，
所以∠BEC=60°+35°=95°
习题5.4第9题答案
120°
解析：∵∠COE= 90°，
∴∠DOE ＝90°
∵∠EOF＝120°，
∴∠DOF＝ 30°
∵OD平分∠BOF，
∴∠BOF＝ 60°
∴∠AOF=180°-60°=120°
习题5.4第10题答案
解：（1）如图5-5-33（1）所示，
过C作CD∥AB
∵AB∥EF，
∴CD∥EF（如果两条直线都与第三条直线平行，那么这两条直线互相平行）
∠B＝∠BCD，∠DCF=∠F（两直线平行，内错角相等）
∴∠BCF=∠B＋∠F(等量代换)
（2）当点C在直线BF的右侧时，∠B ＋∠F+∠BCF=360°
理由如下：过C点作CD∥AB（如图5- 5-33（2）所示）
∵AB∥EF，
∴CD∥EF(如果两条直线都与第三条直线平行，那么这两条直线互相平行)
∴∠B+∠BCD=180°，∠F+∠DCF ＝ 180°（两直线平行，同旁内角互补）
∴∠B+∠BCD+ ∠F+∠DCF＝ 360°（等量代换），
即∠B+∠F＋∠BCF=360°
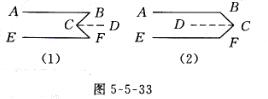
习题5.4第11题答案
解：∵AB∥CD(已知)，
∴∠ECD=∠A =40°（两直线平行，同位角相等）
∵DE上AE(已知)，
∴∠CED= 90°（垂直定义）
又∵∠D+∠ECD+∠CED=180°（三角形内角和是180°），
∴∠D ＝ 180°－ ∠ECD - ∠CED
＝ 180°-40°-90°＝50°
苏科版七年级下册数学书答案
北师大版七年级下册数学书答案
语文版七年级下册语文课本答案
浙教版七年级下册科学课本答案
浙教版七年级下册数学课本答案
北师大版七年级下册生物课本答案
北师大版七年级下册历史课本答案
北师大版七年级下册语文课本答案
苏教版七年级下册语文课本答案
七年级下册数学书答案人教版
青岛版七年级上册数学书答案
北师大版七年级上册数学书答案
七年级下册英语同步精练答案外研版
七年级上册数学学法大视野答案湘教版
浙教版七年级上册数学书答案
七年级下册生物长江全能学案同步练习册答案人教版
七年级下册生物同步导学与优化训练答案人教版
七年级下册英语课时特训答案人教版
人教版七年级上册数学课时练答案
七年级下册地理同步精练答案人教版