青岛版数学书八年级下册第34页综合练习答案(3)

第34页综合练习第11题答案

证明：∵四边形ABCD是平行四边形， 

∴AD//BC，

∴∠DAF=∠AFB

又∵AF平分∠BAD，

∴∠DAF=∠BAF， 

∴∠BAF=∠AFB

∴AB=BF 

同理，EC= DC 

∵AB=DC 

∴BF=EC 

∴ BF-EF=EC-EF，即BE=FC

第34页综合练习第12题答案

解：（1）当AD=2AB时，四边形PEMF是矩形， 

证明如下：∵AD= 2AB，M是AD的中点， 

∴AB=AM，CD=DM 

∴∠AMB=∠ABM=45°， ∠DMC=∠DCM=45°， 

∴∠BMC= 90°

又∵PE⊥MC，PF_⊥MB， 

∴∠MEP=∠MFP= 90°， 

∴四边形PEMF是矩形． 

（2）当P是BC的中点时，四边形PEMF是正方形， 

证明知下：∵P是BC的中点，

∴PB=PC 

又∵△MBC为等腰直角三角形， 

∴点P在∠BMC的平分线上， 

∴PE= PF，

∴矩形PEMF是正方形

第34页综合练习第13题答案

（1）证明：∵△BCF和△ABD是等边三角形， 

∴AB= BD，FB=CB，∠DBA=∠FBC=60°， 

∴∠DBF=∠ABC， 

∴△DBF≌△ABC(SAS)，

∴DF=AC 

又∵△ACE是等边三角形， 

∴AE=AC 

∴DF=AE

同理，EF=AD 

∴四边形DAEF是平行四边形

（2）解：当∠BAC= 150°时，四边形DAEF是矩形；

当AB=AC且∠BAC≠60°时，四边形DAEF是菱形；

当∠BAC=150°且AB=AC时，四边形DAEF是正方形。

第34页综合练习第14题答案

证明：如图6-5-22所示．

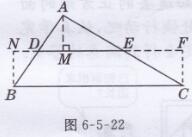
由剪切和拼接方法知AM⊥DE且△ADM≌△BDN 

∴∠N=∠AMD=90°， ∠NBD+∠ABC= 90°

同理，∠F=∠AME=90°

又∵DE//BC，BN//CF， 

∴四边形NBCF是平行四边形， 

∵∠F=90°， 

∴四边形NBCF是矩形

第34页综合练习第15题答案

（1）证明：∵EF//BC，

∴∠OEC=∠BCE 

又∵CE平分∠ACB， 

∴∠OCE=∠BCE 

∴∠OEC= ∠OCE 

∴EO=OC

同理，OF=OC 

∴EO= OF 

（2）解：当点O是AC的中点时，四边形AECF是矩形，

∵EO=OF, OA=OC, 

∴四边形AECF是平行四边形

又∵CE平分∠ACB，CF平分∠ACD， 

∴∠ACE+∠ACF= 90°， 

即∠ECF= 90°

∴□AECF是矩形

第34页综合练习第16题答案

（1）证明：∵四边形ABCD是正方形， 

∴∠ADC=∠C= 90°，AD=DC=BC 

∵BE=CF 

∴DF=CE 

∴△ADF≌△DCE(SAS) 

∴AF=DE, ∠DAF=∠CDE 

∵∠CDE+∠ADE= 90°， 

∴∠ADE+∠DAF=90°, 

∴∠AGD=90°，即AF⊥DE 

（2）解：成立， 

证明：∵四边形ABCD是正方形， 

∴AD=DC=BC, ∠ADC=∠DCB= 90° 

∵BE=CF

∴DF= CE 

∴△ADF≌△DCE(SAS) 

∴AF=DE, ∠DAF=∠CDE 

∵∠CDE+∠ADE= 90°， 

∴∠ADE+∠DAF=90°， 

∴∠AGD=90°，即AF⊥DE 

（3）解：四边形MNPQ是正方形。

由（2）知AF⊥DE且AF=DE 

∵M，N，P，Q分别为AE，EF, FD，AD的中点， 

∴由三角形中位线知

MN=QP=1/2AF，MQ=NP=1/2DE

∴MN=QP=MQ=NP, 

∴四边形MNPQ是菱形 

又由三角形中位线知MN//AF, NP//DE, 

∵AF⊥DE, 

∴MN⊥NP， 

∴菱形MNPQ是正方形