第34页综合练习第6题答案
解：如图6-5-19所示，连接AB
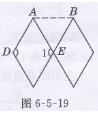
∵AB=18 cm，AE=18 cm，BE=18 cm，
∴△ABE是等边三角形，
∴∠AEB=60°，
∴∠1=120°
又∵菱形中∠D=∠1，
∴∠D=120°
第34页综合练习第7题答案
解：由题意可知：AB=FG, BC=GA, ∠B=∠G，
∴△ABC≌△FGA(SAS)．
∴∠BAC=∠GFA
又∵∠GFA+∠GAF= 90°，
∴∠BAC+∠GAF= 90°
∴∠FAC=90°
又∵△ABC≌△FGA
∴AC=AF
∴△ACF是等腰直角三角形，
∴∠FCA=45°
第34页综合练习第8题答案
（1）证明：∵四边形ABCD是正方形，
∴CB=CD, ∠BCE=∠DCF
又∵CE= CF，
∴△BCE≌△DCF(SAS)
（2）解：由(1)知△BCE≌△DCF，
∴∠DFC=∠BEC
又∵∠BEC=60°，
∴∠DFC= 60°
由CE=CF, ∠DCF=90°，
∴∠EFC=45°
∴∠EFD= ∠CFD-∠EFC=60°-45°=15°
第34页综合练习第9题答案
证明：如图6-5-20所示，
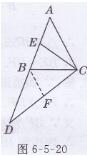
过点B作△BDC的中线BF交CD于点F
∴BF=1/2AC=1/2AB
又∵E是AB的中点，
∴BE=1/2AB
∴BE=BF
∵AB=AC
∴∠ABC=∠ACB=∠FBC
又∵BC=BC，
∴△EBC≌△FBC(SAS)
∴EC= FC=1/2 CD
∴CD=2CE
第34页综合练习第10题答案
解：能取CD的中点E，连接AE, BE，则△ABE是直角三角形，如图6-5-21所示
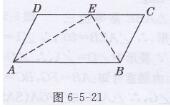
证明如下：∵E是CD的中点，DC=2DE
∵AD:AB=1:2．
∴AB=2AD
∵AB=DC
∴DC= 2AD
∴AD=DE,
∴∠DAE=∠DEA
∵DE//AB，
∴∠DEA=∠BAE,
∴∠DAE=∠BAE.
∴AE平分∠BAD，
∴∠BAE=1/2∠BAD
同理，∠ABE=1/2∠ABC
∵AD∥BC，
∴∠BAD+ ∠ABC=180°
∴∠BAE+∠ABE
=1/2∠BAD+1/2∠ABC
=1/2（∠BAD+∠ABC）
=90°
∴△AEB为直角三角形
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
八年级下册数学课时特训答案浙教版
八年级上册物理配套练习册答案沪科版
苏教版八年级上册思想品德补充习题答案
苏教版八年级上册语文补充习题答案
华东师大版八年级上册数学书答案
八年级下册思想品德同步精练答案粤教版
八年级下册数学同步精练答案北师大版
八年级下册物理伴你学答案苏科版
人教版八年级上册地理长江作业本答案
八年级上册语文同步训练答案人教版