习题17.1第11题答案
解：Rt△ABC中，∵∠A=30°，∴BC= 1/2AB，
由勾股定理，得AB2=BC2 +AC2
∴AB2=(1/2AB) 2+22，
∴3/4AB2 =4，
∴AB2=16/3
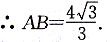
习题17.1第12题答案
解：因为5个边长为1的正方形的面积和是5，所以拼成的正方形边长应为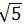
，
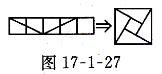
所以原图的分割与拼接如图17-1-27所示
习题17.1第13题答案
证明：∵△ACD是等腰直角三角形，
∴由勾股定理，得AD2 =AC2 +CD2
由圆面积公式，得
S半圆ACD=1/2π（AD/2)2=1/8πAD2，
S半圆AEC=1/2π（AC/2）2= 1/8πAC2
S半圆CFD=1/2π（CD/2）2=1/8πCD2，
∴S弓形AGC +S弓形CHD =S半圆ACD -S△ACD，
∴S月形AGCE +S月形DHCF
=S半圆AEC +S半圆CFD -（S弓形AGC +S弓形CHD）
=S半圆AEC +S半圆CFD -（S半圆ACD - S△ACD）
=1/8πAC2+1/8πCD2-1/8πAD2+S△ACD
=1/8π（AC2+CD2）-1/8πAD2+S△ACD
=1/8πAD2-1/8πAD2+S△ACD
= S△ACD
习题17.1第14题答案
证明：如图17- 1-28所示，连接BD
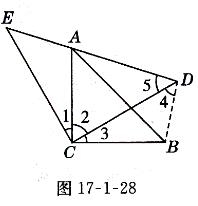
∵△ACB和△ECD都是等腰直角三角形，
∴CE=CD, CA=CB, ∠ECD＝ ∠ACB＝90°,
∴∠1＋∠2=∠2+∠3＝90°，
∴∠1=∠3，
∴△ACE≌△BCD
∴AE=BD，∠4＝∠E＝∠5＝45°，
∴∠4+∠5＝ 90°，即∠ADB=90°
在Rt△ADB中，由勾股定理，得
AB2=BD2+AD2=AE2+AD2
在Rt△ACB中，由勾股定理，得
AB2=AC2+BC2=2AC2
∴AE2 +AD2 =2AC2
苏科版八年级下册数学书答案
北师大版八年级下册数学书答案
八年级下册物理书答案北师大版
译林牛津版八年级下册英语课本答案
苏教版八年级下册语文课本答案
人教版八年级下册英语课本答案
北师大版八年级下册生物课本答案
北师大版八年级下册历史课本答案
浙教版八年级下册科学课本答案
人教版八年级下册生物课本答案
人教版八年级上册英语作业本答案
人教版八年级上册英语课时特训答案
华东师大版八年级上册数学书答案
人教版八年级上册语文作业本答案
八年级上册语文课课练答案苏教版
八年级下册英语作业本答案人教版
八年级下册思想品德课课练答案苏人版
教科版八年级上册物理作业本答案江西省
八年级下册数学课时作业本答案人教版
八年级下册历史与社会思想品德课时特训答案人教版