一元二次……关系第9题答案
解：设方程的两个实数根为x₁，x₂，
则x₁+x₂=2（m-2），x₁•x₂=m2
令x₁2+ x₂2=56，得
（x₁+x₂）2- 2 x₁x₂=4（m-2）2 -2m2 =56，
解这个方程得，m-10或m=-2
当m=10时，△<0，所以不合题意，应舍去，
当m=-2时，△>0，符合题意，
所以存在实数m=-2，使得方程的两个实数根的平方和等于56
一元二次……关系第10题答案
解：设边AB=a，AC=b，
∵a，b是方程x2-（2k+3）x+k2+3k+2=0的两根，
∴a+b=2k+3，a•b=k2+3k+2
又∵△ABC是以BC为斜边的直角三角形，且BC=5，
∴a2 +b2=52，即（a+b）2-2ab=52，
∴（2k+3）2-2（k2+3k+2） =25，
∴k2+3k-10=0，
∴k₁=-5或k₂=2
当k=-5时，方程为x2+7x+12=0，解得x₁=-3，x₂=-4（舍去）；
当k=2时，方程为x2-7x+12=0，解得x₁=3，x₂=4
∴当k=2时，△ABC是以BC为斜边的直角三角形
一元二次……关系第11题答案
解：（1）∵方程有实数解，
∴b2-4ac=22 -4（k+1）≥0，解得k≤0
∴k的取值范围是k≤0
（2）根据一元二次方程根与系数的关系得
x₁+x₂=-2，x₁x₂=k+1
∴x₁+x₂- x₁x₂=-2-（k+1）
由已知，得2-k-1<-1，解得k> -2
又由（1）得k≤0，∴-2<k≤0
∵k为整数，
∴k的值为-1或0
一元二次……关系第12题答案
解：∵关于x的一元二次方程4x2 +4（m-1）x+m2 =0有两个非零实数根，
∴b2 -4ac=[4（m-1）]2 -4×4m2= -32m+16≥0，
∴m≤1/2
又x₁，x₂是方程4x2+4（m-1）x+m2 =0的两个实数根，
∴由一元二次方程根与系数的关系，得：
x₁+x₂=-（m-1），x₁•x₂=（1/4）m2
假设x₁，x₂同号，则有两种可能：
（1）x₁<0，x₂<0；
（2）x₁>0，x₂>0
若x₁<0 ，x₂<0
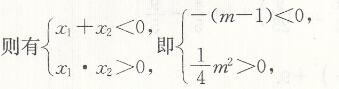
解这个不等式组得m>1
∵m≤1/2时方程才有实数根，
∴此种情况不成立
若x₁>0，x₂>0，
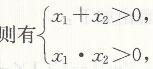
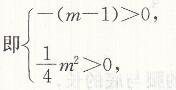
解这个不等式组，得m<1
又∵m≤1/2，
∴当m≤1/2时，两根能同号
数学九年级上册轻轻松松学数学冀教版
九年级上册化学课本答案沪教版
华东师大版九年级上册数学书答案
人教版九年级上册化学书答案
人教版九年级上册物理书答案
人教版九年级上册英语书答案
浙教版九年级上册科学书答案
沪科版九年级上册数学书答案
浙教版九年级上册数学书答案
人教版九年级上册语文书答案
北师大版九年级上册数学书答案
苏科版九年级上册数学书答案
九年级下册思想品德课时练答案人教版
人教版九年级上册语文知识与能力训练答案
人教版九年级下册语文作业本答案江西省
人教版九年级上册语文作业本答案
九年级上册思想品德课课练答案苏人版
九年级下册数学课时练答案人教版
人教版九年级下册数学南方新课堂答案
沪教版英语书九年级下册答案
九年级上册物理学法大视野答案人教版