冀教版九年级上册数学第二十三章23.4用样本估计总体轻轻松松学数学答案(2)

用样本估计总体第12题答案

解：（1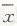）=1/10×（2.0×1+2.2×2+2.4×3+2.5×2+2.6×1+3.0×1）=2.42（千克）

（2）从抽取的样本中知道，10只鸡中能出售的有9只，占90%，估计这1000只鸡中能出售的为1000×90% =900（只）

用样本估计总体第13题答案

解：（1）抽取的男生总数为6+10+16+12+6=50（人）

（2）身高在164.5 cm～169.5 cm范围内男生人数最多

（3）全校男生身高在170 cm及170 cm以上的人数为300×（12+6）/50=108（人）

用样本估计总体第14题答案

解：（1）∵（540+450+300×2+240×6+210×3+ 120×2）÷15 =3900÷15=260（件）， 

∴这15名工人该月加工零件数的平均数为260件 

∵数据由低到高排序为120，120，210，210．210，240，240， 240，240， 240， 240， 300，300，450，540， 

∴中位数为240件， 

∵240件出现的次数最多，为6次，∴众数为240件 

（2）工作任务确定为260件不合理。理由如下：

由题意知，每月能完成260件的人数是4人，有11人不能完成此任务，尽管260件是平均数，但不利于调动工人的积极性，而240件既是中位数，又是众数，故工作任务确定为240件较合理

用样本估计总体第15题答案

解：（1）根据样本平均数、方差公式，中位数、众数的定义，不难从图中提供的各次成绩求出张明同学的平均成绩为80分，方差为60分，王成的平均成绩为80分，中位数为85分，众数为90分； 

（2）若将90分以上（含90分）的成绩视为优秀，则10次单元自我检测成绩中，张明同学仅有3次成绩达到优秀，而王成同学有5次成绩达到优秀，因此，优秀率高的是王成。

（3）尽管王成同学优秀率高，但他的成绩不稳定（方差大）。而张明同学虽然优秀率比不上王成同学，但他的考试成绩相对稳定，根据两位同学10次检测的成绩 看，发现他们各有所长，也各有所短，因此，如何切合实际、准确地为他们今后提出合理化的学习建议显得尤为重要，下面给出一条仅供参考：王成同学要持之以恒，保持稳定；张明同学的学习还要加一把劲，提高优秀率。

用样本估计总体第16题答案

解：（1）a=10，b=3，c=0.15.频数分布直方图如图D-23-2所示

（2）从样本中PM2.5的24小时平均浓度不低于50微克／立方米的5天中抽取2天 的所有的结果为：b₁b₂，b₁b₃，b₂d₃，b₁d₂，b₂d₁，b₂ d₂，b₃d₁，b₃ d₂，b₁b₂， 共10种，其中恰好有一天PM2.5的24小时平均浓度不低于75微克／立方米的结果为：b₁d₁，b₂d₃，b₂ d₁，b₂ d₂，b₂ d₂，b₃ d₁，b₃ d₂，共6种，则恰好有一天PM2.5的24小时平均浓度不低于75微克／立方米的频率为：P=6/10 = 3/5 

（3）该居民区去年的环境需要改进。理由如下：

去年该居民区PM2.5的年平均浓度为：

（12.5×5+37.5×10+62.5×3+87.5×2）÷20=40（微克／立方米）

因为40>35，所以去年该居民区PM2.5的年平均浓度不符合《环境空气质量标准》，故该居民区去年的环境需要改进。

用样本估计总体第17题答案

解：（1）（11+18+16）÷（1-10%）=50（名），50-11-18-16=5（名），

∴在这次调查中，最喜欢新闻类电视节目的学生有5名，

补全条形图如图D-23-3所示  

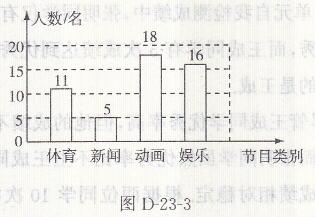
（2）1200×11/50=264（名）， 

∴估计全校学生中最喜欢体育类电视节目的学生有264名